题目内容
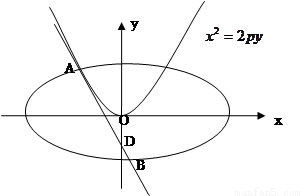
如图,已知点D(0,-2),过点D作抛物线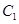 :
: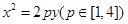 的切线l,切点A在第二象限。
的切线l,切点A在第二象限。
(1)求切点A的纵坐标;
(2)若离心率为 的椭圆
的椭圆 恰好经过A点,设切线l交椭圆的另一点为B,若设切线l,直线OA,OB的斜率为k,
恰好经过A点,设切线l交椭圆的另一点为B,若设切线l,直线OA,OB的斜率为k,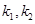 ,①试用斜率k表示
,①试用斜率k表示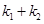 ②当
②当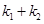 取得最大值时求此时椭圆的方程。
取得最大值时求此时椭圆的方程。
【答案】
1)设切点A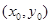 ,依题意则有
,依题意则有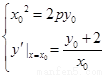 解得
解得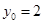 ,即A点的纵坐标为2
,即A点的纵坐标为2
(2)依题意可设椭圆的方程为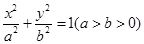 ,直线AB方程为:
,直线AB方程为: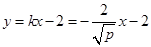 ;由
;由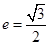 得
得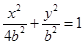 ①
①
由(1)可得A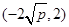 ,将A代入①可得
,将A代入①可得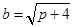 ,故椭圆的方程可简化为
,故椭圆的方程可简化为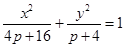 ;
;
联立直线AB与椭圆的方程: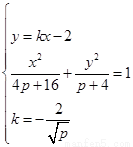 消去Y得:
消去Y得: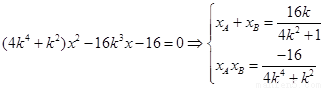 ,则
,则
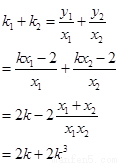
又∵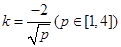 ,∴k∈[-2,-1];即
,∴k∈[-2,-1];即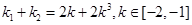
(3)由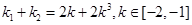 可知
可知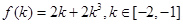 上为单调递增函数,故当k=-1时,
上为单调递增函数,故当k=-1时,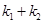 取到最大值,此时P=4,故椭圆的方程为
取到最大值,此时P=4,故椭圆的方程为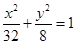
【解析】略

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 (2012•黄州区模拟)如图,已知点D(0,-2),过点D作抛物线C1:x2=2py(p∈[1,4]的切线l,切点A在第二象限.
(2012•黄州区模拟)如图,已知点D(0,-2),过点D作抛物线C1:x2=2py(p∈[1,4]的切线l,切点A在第二象限.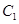 :
: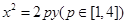 的切线
的切线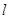 ,切点A在第二象限。
,切点A在第二象限。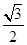 的椭圆
的椭圆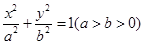 恰好经过A点,设切线l交椭圆的另一点为B,若设切线
恰好经过A点,设切线l交椭圆的另一点为B,若设切线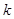 ,
,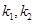 ,①试用斜率k表示
,①试用斜率k表示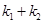 ②当
②当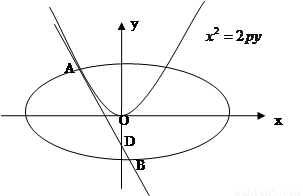
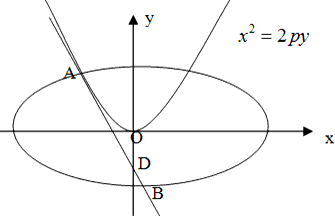 如图,已知点D(0,-2),过点D作抛物线C1:x2=2py(p∈[1,4]的切线l,切点A在第二象限.
如图,已知点D(0,-2),过点D作抛物线C1:x2=2py(p∈[1,4]的切线l,切点A在第二象限. 的椭圆
的椭圆 +
+ =1(a>b>c)恰好经过A点,设切线l交椭圆的另一点为B,若设切线l,直线OA,OB的斜率为k,k1,k2,①试用斜率k表示k1+k2②当k1+k2取得最大值时求此时椭圆的方程.
=1(a>b>c)恰好经过A点,设切线l交椭圆的另一点为B,若设切线l,直线OA,OB的斜率为k,k1,k2,①试用斜率k表示k1+k2②当k1+k2取得最大值时求此时椭圆的方程. 的椭圆
的椭圆 恰好经过A点,设切线l交椭圆的另一点为B,若设切线l,直线OA,OB的斜率为k,k1,k2,
恰好经过A点,设切线l交椭圆的另一点为B,若设切线l,直线OA,OB的斜率为k,k1,k2,