题目内容
 (2012•黄州区模拟)如图,已知点D(0,-2),过点D作抛物线C1:x2=2py(p∈[1,4]的切线l,切点A在第二象限.
(2012•黄州区模拟)如图,已知点D(0,-2),过点D作抛物线C1:x2=2py(p∈[1,4]的切线l,切点A在第二象限.(1)求切点A的纵坐标;
(2)若离心率为
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
分析:(1)设切点A的坐标,得切线的方程,根据点D(0,-2)在l上,从而可求切点A的纵坐标;
(2)先根据e=
及A(-2
,2),化简椭圆方程,设直线AB方程椭圆的方程,消去y,利用韦达定理可求斜率,利用函数的单调性,可求最值,从而可得椭圆的方程.
(2)先根据e=
| ||
| 2 |
| p |
解答:解:(1)设切点A(x0,y0),依题意则有y0=
,
由切线l的斜率为k=
,得l的方程为y=
x-
,
又点D(0,-2)在l上,
∴
=2,即点A的纵坐标y0=2;
(2)依题意可设直线AB方程为:y=kx-2=-
x-2;
由e=
得
+
=1
由(1)可得A(-2
,2),将A代入
+
=1可得b=
,故椭圆的方程可简化为
+
=1;
联立直线AB与椭圆的方程,消去y得:(4k4+k2)x2-16k3x-16=0
设A(x1,y1),B(x2,y2),则x1+x2=
,x1x2=
①k1+k2=
+
=2k-2×
=2k+2k3;
②∵k=
(p∈[1,4]),∴k∈[-2,-1],
∵f(k)=2k+2k3在[-2,-1]上为单调递增函数,故当k=-1时,k1+k2取到最大值,此时P=4,
故椭圆的方程为
+
=1.
| x02 |
| 2p |
由切线l的斜率为k=
| x0 |
| p |
| x0 |
| p |
| x02 |
| 2p |
又点D(0,-2)在l上,
∴
| x02 |
| 2p |
(2)依题意可设直线AB方程为:y=kx-2=-
| 2 | ||
|
由e=
| ||
| 2 |
| x2 |
| 4b2 |
| y2 |
| b2 |
由(1)可得A(-2
| p |
| x2 |
| 4b2 |
| y2 |
| b2 |
| p+4 |
| x2 |
| 4p+16 |
| y2 |
| p+4 |
联立直线AB与椭圆的方程,消去y得:(4k4+k2)x2-16k3x-16=0
设A(x1,y1),B(x2,y2),则x1+x2=
| 16k |
| 4k2+1 |
| -16 |
| 4k4+k2 |
①k1+k2=
| kx1-2 |
| x1 |
| kx2-2 |
| x2 |
| x1+x2 |
| x1x2 |
②∵k=
| -2 | ||
|
∵f(k)=2k+2k3在[-2,-1]上为单调递增函数,故当k=-1时,k1+k2取到最大值,此时P=4,
故椭圆的方程为
| x2 |
| 32 |
| y2 |
| 8 |
点评:本题主要考查抛物线的切线方程,考查直线与椭圆的位置关系及利用函数的单调性求最值,属于中档题.

练习册系列答案
相关题目
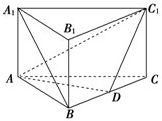 (2012•黄州区模拟)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1,∠ABC=90°,D是BC的中点.
(2012•黄州区模拟)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1,∠ABC=90°,D是BC的中点. (2012•黄州区模拟)已知某几何体的三视图如图,则该几何体的表面积为
(2012•黄州区模拟)已知某几何体的三视图如图,则该几何体的表面积为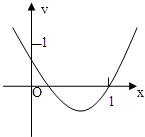 (2012•黄州区模拟)如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=2lnx+f(x)在点(b,g(b))处切线的斜率的最小值是( )
(2012•黄州区模拟)如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=2lnx+f(x)在点(b,g(b))处切线的斜率的最小值是( )