题目内容
 (2012•葫芦岛模拟)如图,椭圆C:
(2012•葫芦岛模拟)如图,椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆C的方程;
(2)设直线AF1与椭圆交于另一点B,与y轴交于一点C,记m=
| S△AF1O |
| S△ACO |
| S△BF1O |
| S△BCO |
分析:(1)根据F1,F2是A1A2的三等分点,可得a=3c,利用|AF1|+|AF2|=6,可得a=3,从而可得椭圆C的方程;
(2)当直线与x轴重合时,显然不合题意;当直线不与x轴重合时,设直线AF1的方程代入到椭圆方程并消元整理利用韦达定理及C点坐标,确定m=
=
,n=
=
,由此可确定m+n的取值范围.
(2)当直线与x轴重合时,显然不合题意;当直线不与x轴重合时,设直线AF1的方程代入到椭圆方程并消元整理利用韦达定理及C点坐标,确定m=
| S△AF1O |
| S△ACO |
| my1 |
| my1-1 |
| S△BF1O |
| S△BCO |
| my2 |
| my2-1 |
解答:解:(1)∵F1,F2是A1A2的三等分点,∴a=3c
又∵|AF1|+|AF2|=6,∴a=3
∴c=1,∴b2=8
∴椭圆C的方程为:
+
=1…(4分)
(2)F1(-1,0),当直线与x轴重合时,显然不合题意,
当直线不与x轴重合时,设直线AF1的方程为:x=my-1
代入到椭圆方程并消元整理得:(8m2+9)y2-16my-64=0 …①
△=162×9(m2+1)>0恒成立;
设A(x1,y1),B(x2,y2),则y1,y2是方程①的两个解,由韦达定理得:y1+y2=
,y1y2=-
在x=my-1中,令x=0得C点坐标为(0,
)…(7分)
m=
=
=
=
(∵A在第一象限,∴x1=my1-1>0,y1>0)
同理:n=
=
…(9分)
∴m+n=
+
=
=
=2+
∵A在第一象限,∴C点在椭圆内部
∴0<
<2
,∴m2>
∴8m2-1>0,∴m+n>2
∴m+n的取值范围是(2,+∞)…(12分)
又∵|AF1|+|AF2|=6,∴a=3
∴c=1,∴b2=8
∴椭圆C的方程为:
| x2 |
| 9 |
| y2 |
| 8 |
(2)F1(-1,0),当直线与x轴重合时,显然不合题意,
当直线不与x轴重合时,设直线AF1的方程为:x=my-1
代入到椭圆方程并消元整理得:(8m2+9)y2-16my-64=0 …①
△=162×9(m2+1)>0恒成立;
设A(x1,y1),B(x2,y2),则y1,y2是方程①的两个解,由韦达定理得:y1+y2=
| 16m |
| 8m2+9 |
| 64 |
| 8m2+9 |
在x=my-1中,令x=0得C点坐标为(0,
| 1 |
| m |
m=
| S△AF1O |
| S△ACO |
| |AF1| |
| |AC| |
| ||||
|
| my1 |
| my1-1 |
同理:n=
| S△BF1O |
| S△BCO |
| my2 |
| my2-1 |
∴m+n=
| my1 |
| my1-1 |
| my2 |
| my2-1 |
| my1(my2-1)+my2(my1-1) |
| (my1-1)(my2-1) |
| m2y1y2-m(y1+y2) |
| m2y1y2-m(y1+y2)+1 |
| 2 |
| 8m2-1 |
∵A在第一象限,∴C点在椭圆内部
∴0<
| 1 |
| m |
| 2 |
| 1 |
| 8 |
∴8m2-1>0,∴m+n>2
∴m+n的取值范围是(2,+∞)…(12分)
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查三角形面积的计算,确定m,n的表示是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
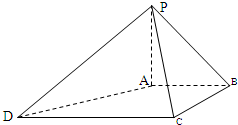 (2012•葫芦岛模拟)在四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,AB⊥BC,PA=AB=BC=
(2012•葫芦岛模拟)在四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,AB⊥BC,PA=AB=BC=