ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΝΫœΊ≥«![]() ΚΆ
ΚΆ![]() œύΨύ
œύΨύ![]() Θ§œ÷ΦΤΜ°‘ΎΝΫœΊ≥«ΆβΈΜ”ΎœΏΕΈ
Θ§œ÷ΦΤΜ°‘ΎΝΫœΊ≥«ΆβΈΜ”ΎœΏΕΈ![]() …œ―Γ‘ώ“ΜΒψ
…œ―Γ‘ώ“ΜΒψ![]() Ϋ®‘λ“ΜΗωΝΫœΊ≥«ΒΡΙΪΙ≤ά§Μχ¥Πάμ≥ßΘ§“―÷Σά§Μχ¥Πάμ≥ßΕ‘≥« –ΒΡ”ΑœλΕ»”κΥυ―ΓΒΊΒψΒΫ≥« –ΒΡΒΡΨύάκΙΊœΒΉν¥σΘ§ΤδΥϊ“ρΥΊ”ΑœλΫœ–Γ‘ί ±≤ΜΩΦ¬«Θ§ά§Μχ¥Πάμ≥ßΕ‘≥«
Ϋ®‘λ“ΜΗωΝΫœΊ≥«ΒΡΙΪΙ≤ά§Μχ¥Πάμ≥ßΘ§“―÷Σά§Μχ¥Πάμ≥ßΕ‘≥« –ΒΡ”ΑœλΕ»”κΥυ―ΓΒΊΒψΒΫ≥« –ΒΡΒΡΨύάκΙΊœΒΉν¥σΘ§ΤδΥϊ“ρΥΊ”ΑœλΫœ–Γ‘ί ±≤ΜΩΦ¬«Θ§ά§Μχ¥Πάμ≥ßΕ‘≥«![]() ΚΆ≥«
ΚΆ≥«![]() ΒΡΉή”ΑœλΕ»ΈΣΕ‘≥«
ΒΡΉή”ΑœλΕ»ΈΣΕ‘≥«![]() ”κ≥«
”κ≥«![]() ΒΡ”ΑœλΕ»÷°ΚΆ. Φ«
ΒΡ”ΑœλΕ»÷°ΚΆ. Φ«![]() ΒψΒΫ≥«
ΒψΒΫ≥«![]() ΒΡΨύάκΈΣ
ΒΡΨύάκΈΣ![]() Θ§Ϋ®‘Ύ
Θ§Ϋ®‘Ύ![]() ¥ΠΒΡά§Μχ¥Πάμ≥ßΕ‘≥«
¥ΠΒΡά§Μχ¥Πάμ≥ßΕ‘≥«![]() ΚΆ≥«
ΚΆ≥«![]() ΒΡΉή”ΑœλΕ»ΈΣ
ΒΡΉή”ΑœλΕ»ΈΣ![]() Θ§Ά≥ΦΤΒς≤ι±μΟςΘΚά§Μχ¥Πάμ≥ßΕ‘≥«
Θ§Ά≥ΦΤΒς≤ι±μΟςΘΚά§Μχ¥Πάμ≥ßΕ‘≥«![]() ΒΡ”ΑœλΕ»”κΥυ―ΓΒΊΒψΒΫ≥«
ΒΡ”ΑœλΕ»”κΥυ―ΓΒΊΒψΒΫ≥«![]() ΒΡΨύάκΒΡΤΫΖΫ≥…Ζ¥±»Θ§±»άΐœΒ ΐ2.7ΘΜά§Μχ¥Πάμ≥ßΕ‘≥«
ΒΡΨύάκΒΡΤΫΖΫ≥…Ζ¥±»Θ§±»άΐœΒ ΐ2.7ΘΜά§Μχ¥Πάμ≥ßΕ‘≥«![]() ΒΡ”ΑœλΕ»”κΥυ―ΓΒΊΒψΒΫ≥«
ΒΡ”ΑœλΕ»”κΥυ―ΓΒΊΒψΒΫ≥«![]() ΒΡΨύάκΒΡΤΫΖΫ≥…Ζ¥±»Θ§±»άΐœΒ ΐΈΣ
ΒΡΨύάκΒΡΤΫΖΫ≥…Ζ¥±»Θ§±»άΐœΒ ΐΈΣ![]() ΘΜ«“Β±ά§Μχ¥Πάμ≥ß
ΘΜ«“Β±ά§Μχ¥Πάμ≥ß![]() ”κ≥«
”κ≥«![]() ΨύάκΈΣ
ΨύάκΈΣ![]() ±Ε‘≥«
±Ε‘≥«![]() ΚΆ≥«
ΚΆ≥«![]() ΒΡΉή”ΑœλΕ»ΈΣ0.029.
ΒΡΉή”ΑœλΕ»ΈΣ0.029.
(1) ΫΪ![]() ±μ Ψ≥…
±μ Ψ≥…![]() ΒΡΚ· ΐΘΜ
ΒΡΚ· ΐΘΜ
(2) Χ÷¬έΔ≈÷–Κ· ΐΒΡΒΞΒς–‘Θ§≤Δ≈–Εœ‘ΎœΏΕΈ![]() …œ «Ζώ¥φ‘Ύ“ΜΒψΘ§ ΙΫ®‘Ύ¥Υ¥ΠΒΡά§Μχ¥Πάμ≥ßΕ‘≥«
…œ «Ζώ¥φ‘Ύ“ΜΒψΘ§ ΙΫ®‘Ύ¥Υ¥ΠΒΡά§Μχ¥Πάμ≥ßΕ‘≥«![]() ΚΆ≥«
ΚΆ≥«![]() ΒΡΉή”ΑœλΕ»Ήν–ΓΘΩ»τ¥φ‘ΎΘ§«σ≥ωΗΟΒψΒΫ≥«
ΒΡΉή”ΑœλΕ»Ήν–ΓΘΩ»τ¥φ‘ΎΘ§«σ≥ωΗΟΒψΒΫ≥«![]() ΒΡΨύάκΘΜ»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…Θ°
ΒΡΨύάκΘΜ»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©Κ· ΐ‘Ύ
ΘΜΘ®2Θ©Κ· ΐ‘Ύ![]() ΡΎΒΞΒςΒίΦθΘ§‘Ύ
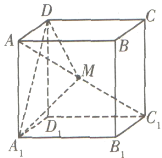
ΡΎΒΞΒςΒίΦθΘ§‘Ύ![]() ΡΎΒΞΒςΒί‘ωΘΜ‘ΎœΏΕΈAB…œ¥φ‘Ύ
ΡΎΒΞΒςΒί‘ωΘΜ‘ΎœΏΕΈAB…œ¥φ‘Ύ![]() ΒψΖϊΚœΧβ“βΘ§ΗΟΒψ”κ≥«
ΒψΖϊΚœΧβ“βΘ§ΗΟΒψ”κ≥«![]() ΒΡΨύάκ
ΒΡΨύάκ![]() .
.
ΓΨΫβΈωΓΩ
Θ®1Θ©œ»«σ≥ωά§Μχ¥Πάμ≥ßΕ‘≥«![]() ΒΡ”ΑœλΕ»±»άΐœΒ ΐ
ΒΡ”ΑœλΕ»±»άΐœΒ ΐ![]() Θ§»ΜΚσΗυΨίΧβ“β«σ
Θ§»ΜΚσΗυΨίΧβ“β«σ![]() ”κ
”κ![]() ΒΡΚ· ΐΙΊœΒΘΜ
ΒΡΚ· ΐΙΊœΒΘΜ
Θ®2Θ©”Π”ΟΒΦ ΐ«σΫβ.
Δ≈ΨίΧβ“βΘ§![]() Θ§
Θ§![]() Θ§
Θ§
![]()
«“Ϋ®‘Ύ![]() ¥ΠΒΡά§Μχ¥Πάμ≥ßΕ‘≥«
¥ΠΒΡά§Μχ¥Πάμ≥ßΕ‘≥«![]() ΒΡ”ΑœλΕ»ΈΣ
ΒΡ”ΑœλΕ»ΈΣ![]() Θ§
Θ§
Ε‘≥«![]() ΒΡ”ΑœλΕ»ΈΣ
ΒΡ”ΑœλΕ»ΈΣ![]() Θ§
Θ§
“ρ¥ΥΉή”ΑœλΕ»![]() Θ°
Θ°
”÷“ρΈΣΒ±ά§Μχ¥Πάμ≥ß![]() ”κ≥«
”κ≥«![]() ΨύάκΈΣ
ΨύάκΈΣ![]() ±
±
Ε‘≥«![]() ΚΆ≥«
ΚΆ≥«![]() ΒΡΉή”ΑœλΕ»ΈΣ0.029.
ΒΡΉή”ΑœλΕ»ΈΣ0.029.
Υυ“‘![]() Θ°
Θ°
Υυ“‘![]() Θ°
Θ°
(2)ΓΓ“ρΈΣ![]() Θ°
Θ°
”…![]() ΫβΒΟ
ΫβΒΟ![]() Θ°
Θ°
”…![]() ΫβΒΟ
ΫβΒΟ![]()
”…![]() ΫβΒΟ
ΫβΒΟ![]()
Υυ“‘![]() Θ§
Θ§![]() Υφ
Υφ![]() ΒΡ±δΜ·«ιΩω»γœ¬±μΘΚ
ΒΡ±δΜ·«ιΩω»γœ¬±μΘΚ
|
|
|
|
|
| 0 |
|
| ®K | ΦΪ–Γ÷Β | ®J |
”…±μΩ…÷ΣΘ§Κ· ΐ‘Ύ![]() ΡΎΒΞΒςΒίΦθΘ§‘Ύ
ΡΎΒΞΒςΒίΦθΘ§‘Ύ![]() ΡΎΒΞΒςΒί‘ωΘ§
ΡΎΒΞΒςΒί‘ωΘ§
Β±![]() ±Θ§
±Θ§![]() Θ§
Θ§
Ι ‘ΎœΏΕΈAB…œ¥φ‘Ύ![]() ΒψΘ§ ΙΒΟΫ®‘Ύ¥Υ¥ΠΒΡά§Μχ¥Πάμ≥ßΕ‘≥«
ΒψΘ§ ΙΒΟΫ®‘Ύ¥Υ¥ΠΒΡά§Μχ¥Πάμ≥ßΕ‘≥«![]() ΚΆ≥«
ΚΆ≥«![]() ΒΡΉή”ΑœλΕ»Ήν–ΓΘ§
ΒΡΉή”ΑœλΕ»Ήν–ΓΘ§
ΗΟΒψ”κ≥«![]() ΒΡΨύάκ
ΒΡΨύάκ![]() Θ°
Θ°