��Ŀ����
[ѡ����]������A��B��C��D�ĸ�С����ֻ��ѡ�����⣬ÿС��10�֣���20�֣�A��ѡ��4-1������֤��ѡ��
��ͼ����O�ǵ���������ABC�����Բ��AB=AC���ӳ�BC����D��ʹCD=AC������AD����O�ڵ�E������BE��AC���ڵ�F���ж�BE�Ƿ�ƽ�֡�ABC����˵�����ɣ�
B��ѡ��4-2��������任
��֪����
 ������M��Ӧ�ı任������y=sinx��Ϊ����C����C�ķ��̣�
������M��Ӧ�ı任������y=sinx��Ϊ����C����C�ķ��̣�C��ѡ��4-4������ϵ���������
��֪����C�ļ����귽����
 ��������C����ͨ���̣�
��������C����ͨ���̣�D��ѡ��4-5������ʽѡ��
��֪x��y��z��R����x+y+z=3����x2+y2+z2����Сֵ��

���𰸡�������A��BEƽ���ABC�����ݵ��������ε����ʣ��ɵá�D=��CAD����ABC=��ACB������ͬ�����Ե�Բ�ܽ���ȣ������ɵ�ABE=��EBC����BEƽ���ABC��
B����P��x��y������������C�ϵ�����һ�㣬��������y=sinx�ϵ�P��x��y���ھ���M�任�µĶ�Ӧ�㣬���ݾ���任�ɵ�y=sinx���Ӷ�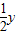 =sin2x���Ӷ���������C�ķ��̣�
=sin2x���Ӷ���������C�ķ��̣�
C������C�ļ����귽��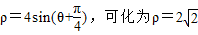 ��sin��+cos�ȣ�������ͬ���Ԧѣ�����ɵ���ͨ���̣�
��sin��+cos�ȣ�������ͬ���Ԧѣ�����ɵ���ͨ���̣�
D��ע�x��y��z��R����x+y+z=3Ϊ��ֵ�����ÿ�������ʽ�õ���x2+y2+z2����12+12+12���ݣ�x×1+y×1+z×1��2=9��
���Ӷ��ý⣮
���A��֤����BEƽ���ABC��
��CD=AC�����D=��CAD��
��AB=AC�����ABC=��ACB��
�ߡ�EBC=��CAD�����EBC=��D=��CAD�� ����5�֣�
�ߡ�ABC=��ABE+��EBC����ACB=��D+��CAD��
���ABE=��EBC����BEƽ���ABC�� ����10�֣�
B���⣺��P��x��y������������C�ϵ�����һ�㣬��������y=sinx�ϵ�P��x��y���ھ���M�任�µĶ�Ӧ�㣬
���� ������5�֣�
������5�֣�
����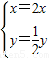 ���ֵ�P��x��y��������y=sinx�ϣ�
���ֵ�P��x��y��������y=sinx�ϣ�
��y=sinx���Ӷ�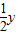 =sin2x��
=sin2x��
��������C�ķ���Ϊy=2sin2x������10�֣�
C���⣺����C�ļ����귽��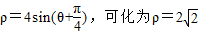 ��sin��+cos�ȣ�������5�֣�
��sin��+cos�ȣ�������5�֣�
��Ϊֱ�����귽��Ϊx2+y2-2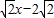 y=0��
y=0��
��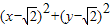 =4������10�֣�
=4������10�֣�
D���⣺ע�x��y��z��R����x+y+z=3Ϊ��ֵ��
���ÿ�������ʽ�õ���x2+y2+z2����12+12+12���ݣ�x×1+y×1+z×1��2=9��
����5�֣�
�Ӷ�x2+y2+z2��3�����ҽ���x=y=z=1ʱȡ��=���ţ�
����x2+y2+z2����СֵΪ3�� ����10�֣�
������������ϵ��4��֪ʶ���������������ѧ������������������
B����P��x��y������������C�ϵ�����һ�㣬��������y=sinx�ϵ�P��x��y���ھ���M�任�µĶ�Ӧ�㣬���ݾ���任�ɵ�y=sinx���Ӷ�
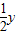 =sin2x���Ӷ���������C�ķ��̣�
=sin2x���Ӷ���������C�ķ��̣�C������C�ļ����귽��
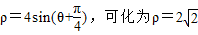 ��sin��+cos�ȣ�������ͬ���Ԧѣ�����ɵ���ͨ���̣�
��sin��+cos�ȣ�������ͬ���Ԧѣ�����ɵ���ͨ���̣�D��ע�x��y��z��R����x+y+z=3Ϊ��ֵ�����ÿ�������ʽ�õ���x2+y2+z2����12+12+12���ݣ�x×1+y×1+z×1��2=9��
���Ӷ��ý⣮
���A��֤����BEƽ���ABC��
��CD=AC�����D=��CAD��
��AB=AC�����ABC=��ACB��
�ߡ�EBC=��CAD�����EBC=��D=��CAD�� ����5�֣�
�ߡ�ABC=��ABE+��EBC����ACB=��D+��CAD��
���ABE=��EBC����BEƽ���ABC�� ����10�֣�
B���⣺��P��x��y������������C�ϵ�����һ�㣬��������y=sinx�ϵ�P��x��y���ھ���M�任�µĶ�Ӧ�㣬
����
 ������5�֣�
������5�֣�����
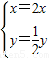 ���ֵ�P��x��y��������y=sinx�ϣ�
���ֵ�P��x��y��������y=sinx�ϣ���y=sinx���Ӷ�
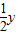 =sin2x��
=sin2x����������C�ķ���Ϊy=2sin2x������10�֣�
C���⣺����C�ļ����귽��
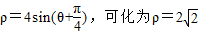 ��sin��+cos�ȣ�������5�֣�
��sin��+cos�ȣ�������5�֣���Ϊֱ�����귽��Ϊx2+y2-2
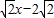 y=0��
y=0����
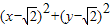 =4������10�֣�
=4������10�֣�D���⣺ע�x��y��z��R����x+y+z=3Ϊ��ֵ��
���ÿ�������ʽ�õ���x2+y2+z2����12+12+12���ݣ�x×1+y×1+z×1��2=9��
����5�֣�
�Ӷ�x2+y2+z2��3�����ҽ���x=y=z=1ʱȡ��=���ţ�
����x2+y2+z2����СֵΪ3�� ����10�֣�
������������ϵ��4��֪ʶ���������������ѧ������������������

��ϰ��ϵ�д�
�����Ŀ
 [ѡ����]������A��B��C��D�ĸ�С����ֻ��ѡ�����⣬ÿС��10�֣���20�֣�
[ѡ����]������A��B��C��D�ĸ�С����ֻ��ѡ�����⣬ÿС��10�֣���20�֣� ѡ���⣺������������С���У���ѡһ���������ȫ����1С�����֣�
ѡ���⣺������������С���У���ѡһ���������ȫ����1С�����֣� �����⣺��ѡ���⣺������A��B��C��D�ĸ�С����ֻ��ѡ�����⣩
�����⣺��ѡ���⣺������A��B��C��D�ĸ�С����ֻ��ѡ�����⣩ �����߶�AC�ij��ȣ�
�����߶�AC�ij��ȣ� ������ֵ��2=2����Ӧ��һ����������
������ֵ��2=2����Ӧ��һ���������� ���������A��
���������A�� �����Dz�����������OΪ���㣬x���������Ϊ���ᣬȡ��ֱ������ϵ����ͬ�ĵ�λ���ȣ�����������ϵ��������C�ļ����귽�̣�
�����Dz�����������OΪ���㣬x���������Ϊ���ᣬȡ��ֱ������ϵ����ͬ�ĵ�λ���ȣ�����������ϵ��������C�ļ����귽�̣�