题目内容
请在下面两题中,任选一题作答:
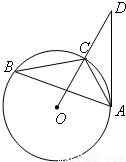
(1)(几何证明选讲选做题)已知PA是圆O的切线,切点为A,PA=2,AC是圆O的直径,PC与圆O交于点B,PB=l,则圆O的半径R=
.
(2)(坐标系与参数方程选做题)已知在极坐标系下两圆的极坐标方程分别为ρ=cosθ,ρ=
sinθ,则此两圆的圆心距为
(1)(几何证明选讲选做题)已知PA是圆O的切线,切点为A,PA=2,AC是圆O的直径,PC与圆O交于点B,PB=l,则圆O的半径R=
| 3 |
| 3 |
(2)(坐标系与参数方程选做题)已知在极坐标系下两圆的极坐标方程分别为ρ=cosθ,ρ=
| 3 |
1
1
.分析:(1)连接AB,根据弦切角定理及三角形相似的判定,我们易得△PBA∽△PAC,再由相似三角形的性质,我们可以建立未知量与已知量之间的关系式,解方程即可求解.
(2)把极坐标方程化为直角坐标方程,求出两圆的圆心坐标,利用两点间的距离公式求出此两圆的圆心距.
(2)把极坐标方程化为直角坐标方程,求出两圆的圆心坐标,利用两点间的距离公式求出此两圆的圆心距.
解答: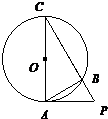 解:(1)依题意,我们知道△PBA∽△PAC,
解:(1)依题意,我们知道△PBA∽△PAC,
由相似三角形的对应边成比例性质我们有
=
,
即R=
=
=
.
故答案为:
.
(2)ρ=cosθ 即 ρ2=ρcosθ,即x2+y2=x,即 (x-
)2+y2=
,
表示以M(
,0)为圆心,以
为半径的圆.
ρ=
sinθ 即 ρ2=
ρ•sinθ,x2+y2=
y,即 x2+(y-
)2=
,
表示以N(0,
)为圆心,以
为半径的圆.
故两圆的圆心距|MN|=
=1,
故答案为:1.
 解:(1)依题意,我们知道△PBA∽△PAC,
解:(1)依题意,我们知道△PBA∽△PAC,由相似三角形的对应边成比例性质我们有
| PA |
| 2R |
| PB |
| AB |
即R=
| PA•AB |
| 2PB |
2
| ||
| 2×1 |
| 3 |
故答案为:
| 3 |
(2)ρ=cosθ 即 ρ2=ρcosθ,即x2+y2=x,即 (x-
| 1 |
| 2 |
| 1 |
| 4 |
表示以M(
| 1 |
| 2 |
| 1 |
| 2 |
ρ=
| 3 |
| 3 |
| 3 |
| ||
| 2 |
| 3 |
| 4 |
表示以N(0,
| ||
| 2 |
| ||
| 2 |
故两圆的圆心距|MN|=
(
|
故答案为:1.
点评:(1)考查圆的切线性质、切割线定理或射影定理,(2)考查极坐标方程与普通方程的互化.

练习册系列答案
相关题目
 (考生注意:请在下面两题中任选一题作答,如果都做,则按所做第1题评分)
(考生注意:请在下面两题中任选一题作答,如果都做,则按所做第1题评分)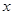 的不等式
的不等式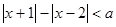 的解集不是空集,求实数
的解集不是空集,求实数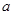 的取值范围;
的取值范围;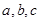 ,满足
,满足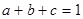 ,求
,求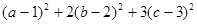 最小值.
最小值.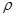 =4cos
=4cos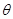 。以极点为平面直角坐标系的原点,极轴为
。以极点为平面直角坐标系的原点,极轴为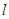 的参数方程是
的参数方程是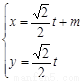 (
(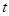 是参数)。
是参数)。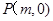 的直线
的直线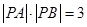 ,试求实数
,试求实数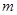 的值。
的值。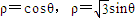 ,则此两圆的圆心距为 .
,则此两圆的圆心距为 .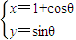 (θ为参数)上的点到曲线C2:
(θ为参数)上的点到曲线C2: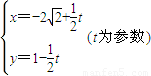 上的点的最短距离为 .
上的点的最短距离为 .