Question

有下列命题：
①a＞b是a²＞b²的充分不必要条件；
②=；
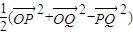③已知f（x）的最大值为M，最小值是m，其值域是[m，M]；
④有3种不同型号的产品A、B、C，其数量之比依次为2：3：4，现用分层抽样方法抽出一个容量为n的样本，样本中A型号产品有10件，则n=90．
其中错误命题的序号为     （要求填写所有错误命题的序号）．

Answer 1

【答案】分析：由充要条件的定义可判断①的真假，根据向量加减法的三角形法则，我们易判断②的对错；函数f（x）不一定是连续函数，由此可判断③的正误；根据分层抽样的方法，我们易得样本容量，进而判断④的对错．
解答：解：当a＞b时，a²＞b²不一定成立，当a²＞b²时，a＞b也不一定成立，故①为假命题；
∵，∴=，故②为真命题；
∵f（x）不一定是连续函数，故当f（x）的最大值为M，最小值是m，其值域不一定是[m，M]，故③为假命题；
∵A、B、C数量之比为2：3：4，又由样本中A型号产品有10件，则n=45．故④为假命题；
故答案：①③④
点评：本题考查的知识点是命题的真假判断与应用，根据充要条件的定义，向量加减法的三角形法则，函数值域与最值的关系，分层抽样的方法，分析题目中的四个结论，易得答案．