题目内容
【题目】已知函数![]() .
.
(1)证明:当![]() 时,
时,![]() ;
;
(2)若![]() 有极大值,求
有极大值,求![]() 的取值范围;
的取值范围;
(3)若![]() 在
在![]() 处取极大值,证明:
处取极大值,证明:![]() .
.
【答案】(1)见证明 (2)![]() (3)见证明
(3)见证明
【解析】
(1)当![]() 时,
时,![]() ,
,![]() ,研究函数的单调性与最值即可证明不等式;
,研究函数的单调性与最值即可证明不等式;
(2)由题设得![]() .由
.由![]() 有极大值得
有极大值得![]() 有解,且
有解,且![]() .利用极大值定义即可建立a的不等关系;
.利用极大值定义即可建立a的不等关系;
(3)由(2)知:当![]() 时,
时,![]() 有唯一的极大值点
有唯一的极大值点![]() , 且
, 且![]() ,故
,故![]() ,结合函数的单调性即可证明.
,结合函数的单调性即可证明.
(1)证明:当![]() 时,
时,![]() ,
,![]() ,
,
令![]() ,则
,则![]() .
.
∴当![]() 时,
时,![]() ,
,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
∴当![]() 时,
时,![]() .
.
∴当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增.
上单调递增.
∴当![]() 时,
时,![]() ,即
,即![]() .
.
(2)解:由题设得![]() .由
.由![]() 有极大值得
有极大值得![]() 有解,且
有解,且![]() .
.
令![]() ,则
,则![]() .由
.由![]() 得
得![]() .
.
∴当![]() 时,
时,![]() ,
,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
∴![]() .
.
当![]() ,即
,即![]() 时,
时,![]() ,即
,即![]() ,此时,
,此时,![]() 在
在![]() 上单调递增,无极值;
上单调递增,无极值;
当![]() ,即
,即![]() 时,
时,
∴![]() ,
,![]() .
.
由(1)知:![]() ,即
,即![]() .
.
∴存在![]() ,
,![]() ,使
,使![]() .
.
∴当![]() 时,
时,![]() ,即
,即![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,
,
即![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,即
,即![]() 单调递增.
单调递增.
∴![]() 是
是![]() 唯一的极大值点.
唯一的极大值点.
综上所述,所求![]() 的取值范围为
的取值范围为![]() .
.
(3)证明:由(2)知:当![]() 时,
时,![]() 有唯一的极大值点
有唯一的极大值点![]() ,
,
且![]() ,故
,故![]() ,
,
由(2)知:![]() .
.
当![]() 时,
时,![]() ,由(2)知:
,由(2)知:![]() 在
在![]() 上单调递增.
上单调递增.
∴当![]() 时,
时,![]() ,即
,即![]() .
.
∴当![]() 时,
时,![]() .
.
综上所述,![]() .
.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案【题目】某企业为了提高企业利润,从2014年至2018年每年都对生产环节的改进进行投资,投资金额![]() (单位:万元)与年利润增长量
(单位:万元)与年利润增长量![]() (单位:万元)的数据如表:
(单位:万元)的数据如表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
投资金额 | 4.0 | 5.0 | 6.0 | 7.0 | 8.0 |
年利润增长量 | 6.0 | 7.0 | 9.0 | 11.0 | 12.0 |
(1)记![]() 年利润增长量
年利润增长量![]() 投资金额,现从2014年至2018年这5年中抽出两年进行调查分析,求所抽两年都是
投资金额,现从2014年至2018年这5年中抽出两年进行调查分析,求所抽两年都是![]() 万元的概率;
万元的概率;
(2)请用最小二乘法求出![]() 关于
关于![]() 的回归直线方程;如果2019年该企业对生产环节改进的投资金额为10万元,试估计该企业在2019年的年利润增长量为多少?
的回归直线方程;如果2019年该企业对生产环节改进的投资金额为10万元,试估计该企业在2019年的年利润增长量为多少?
参考公式: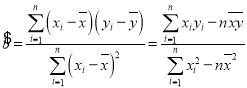 ,
,![]() ;
;
参考数据:![]() ,
,![]() .
.