题目内容
设f(x)=x2-2x-3(x∈R),则在区间[-π,π]上随机取一个实数x,使f(x)<0的概率为
- A.
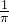
- B.

- C.

- D.

B
分析:解不等式f(x)<0,得不等式的解集区间度为4,而区间[-π,π]的区间长度为2π,由此结合几何概型的公式,不难求出本题的概率.
解答:不等式f(x)<0,即x2-2x-3<0,解之得x∈(-1,3)
∴不等式f(x)<0的解集区间度为3-(-1)=4
∵区间[-π,π]的区间长度为π-(-π)=2π
∴在区间[-π,π]上随机取一个实数x,使f(x)<0的概率为P= =
=
故选B
点评:本题给出函数f(x),求区间[-π,π]上随机取一个实数x,使f(x)<0的概率.着重考查了一元二次不等式的解法和几何概型等知识,属于基础题.
分析:解不等式f(x)<0,得不等式的解集区间度为4,而区间[-π,π]的区间长度为2π,由此结合几何概型的公式,不难求出本题的概率.
解答:不等式f(x)<0,即x2-2x-3<0,解之得x∈(-1,3)
∴不等式f(x)<0的解集区间度为3-(-1)=4
∵区间[-π,π]的区间长度为π-(-π)=2π
∴在区间[-π,π]上随机取一个实数x,使f(x)<0的概率为P=
 =
=
故选B
点评:本题给出函数f(x),求区间[-π,π]上随机取一个实数x,使f(x)<0的概率.着重考查了一元二次不等式的解法和几何概型等知识,属于基础题.

练习册系列答案
相关题目