题目内容
在如图所示的多面体中,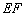 ⊥平面
⊥平面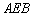 ,
,  ,
,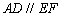 ,
,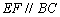 ,
,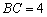 ,
,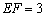 ,
,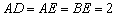 ,
,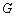 是
是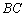 的中点.
的中点.
(1)求证: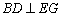 ;
;
(2)求二面角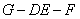 的平面角的余弦值.
的平面角的余弦值.
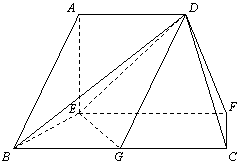
解:(1) 解法1
证明:∵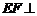 平面
平面 ,
, 平面
平面 ,
,
∴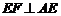 ,
, 

又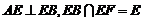 ,
,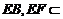 平面
平面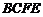 ,
,
∴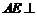 平面
平面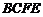 .
.
过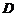 作
作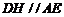 交
交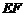 于
于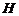 ,则
,则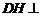 平面
平面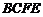 .
.
∵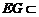 平面
平面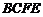 ,
,
∴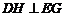 .
.
∵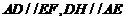 ,∴四边形
,∴四边形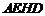 平行四边形,
平行四边形,
∴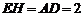 ,
,
∴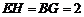 ,又
,又 ,
,
∴四边形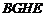 为正方形,
为正方形,
∴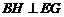 ,
,
又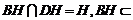 平面
平面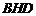 ,
, 平面
平面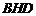 ,
,
∴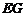 ⊥平面
⊥平面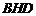 .
.
∵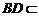 平面
平面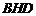 ,
,
∴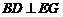 .
.
(2)∵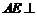 平面
平面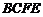 ,
, 平面
平面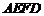
∴平面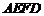 ⊥平面
⊥平面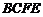
由(1)可知
∴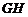 ⊥平面
⊥平面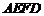
∵ 平面
平面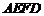
∴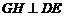
取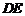 的中点
的中点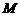 ,连结
,连结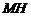 ,
,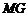
∵四边形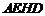 是正方形,
是正方形,
∴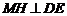
∵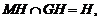
 平面
平面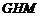 ,
,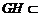 平面
平面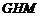
 ∴
∴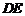 ⊥平面
⊥平面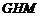
∴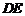 ⊥
⊥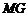
∴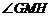 是二面角
是二面角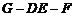 的平面角,
的平面角,
由计算得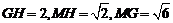
∴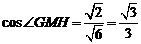
∴平面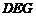 与平面
与平面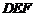 所成锐二面角的余弦值为
所成锐二面角的余弦值为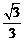 .
.
解法2
∵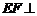 平
平 面
面 ,
, 平面
平面 ,
,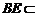 平面
平面 ,
,
∴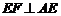 ,
,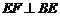 ,
,
又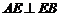 ,
,
∴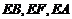 两两垂直.
两两垂直.
以点E为坐标原点,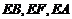 分别为
分别为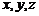 轴
轴
建立如图所示的空间直角坐标系.
由已知得,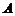 (0,0,2),
(0,0,2),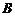 (2,0,0),
(2,0,0),
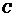 (2,4,0),
(2,4,0), (0,3,0),
(0,3,0),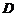 (0,2,2),
(0,2,2),
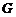 (2,2,0).
(2,2,0).
∴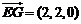 ,
,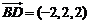 ,
,
∴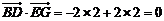 ,
,
∴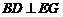 .
.
(2)由已知得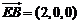 是平面
是平面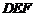 的法向量.
的法向量.
设平面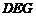 的法向量为
的法向量为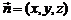 ,
,
∵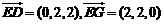 ,
,
∴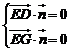 ,即
,即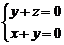 ,令
,令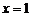 ,得
,得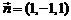 .
.
设平面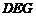 与平面
与平面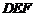 所成锐二面角的大小为
所成锐二面角的大小为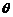 ,
,
则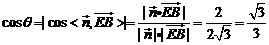
∴平面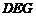 与平面
与平面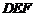 所成锐二面角的余弦值为
所成锐二面角的余弦值为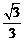 .
.

练习册系列答案
相关题目
 为
为 的内角
的内角 的对边,它的面积为
的对边,它的面积为 ,则角C等于( )
,则角C等于( ) B.
B. C.
C. D.
D.
 的图象关于直线
的图象关于直线 =
= 对称,则函数
对称,则函数 的图象关于直线
的图象关于直线  对称 (B)
对称 (B) 对称 (C)
对称 (C) 对称 (D)
对称 (D) 对称
对称 ”是“
”是“ ”的( )
”的( ) ,命题“
,命题“ ”是 命题(填“真”或“假”).
”是 命题(填“真”或“假”). =
= ,则当
,则当 时左端应在
时左端应在 的基础上加上( )
的基础上加上( )



 .
. .设点
.设点 ,
, ,点
,点 是线段
是线段 上一动点,
上一动点, .当点
.当点 开始运动到点
开始运动到点 结束时,点
结束时,点 所经过的路线长度为 ( )
所经过的路线长度为 ( ) B.
B. C.
C.  D.
D. 
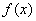 为奇函数,且当
为奇函数,且当 时,
时,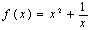 ,则
,则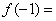 ( )
( ) (B) 0 (C) 1 (D) 2
(B) 0 (C) 1 (D) 2