题目内容
设数列{an}
- A.若
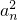 =4n,n∈N*,则{an}为等比数列
=4n,n∈N*,则{an}为等比数列 - B.若an•an+2=
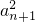 ,n∈N*,则{an}为等比数列
,n∈N*,则{an}为等比数列 - C.若am•an=2m+n,m,n∈N*,则{an}为等比数列
- D.若an•an+3=an+1•an+2,n∈N*,则{an}为等比数列
C
分析:利用等比数列的概念,通过特例法对A,B,C,D四个选项逐一判断排除即可.
解答:A中,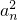 =4n,n∈N*,
=4n,n∈N*,
∴an=±2n,例如2,22,-23,-24,25,26,-27,-28,…不是等比数列,故A错误;
B中,若an=0,满足an•an+2=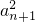 ,n∈N*,但{an}不是等比数列,故B错误;同理也排除D;
,n∈N*,但{an}不是等比数列,故B错误;同理也排除D;
对于C,∵am•an=2m+n,m,n∈N*,
∴ =
= =2,即
=2,即 =2,
=2,
∴{an}为等比数列,故C正确.
故选C.
点评:本题考查等比数列的概念与性质,考查举例排除法的应用,考查分析问题与解决问题的能力,属于中档题.
分析:利用等比数列的概念,通过特例法对A,B,C,D四个选项逐一判断排除即可.
解答:A中,
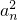 =4n,n∈N*,
=4n,n∈N*,∴an=±2n,例如2,22,-23,-24,25,26,-27,-28,…不是等比数列,故A错误;
B中,若an=0,满足an•an+2=
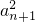 ,n∈N*,但{an}不是等比数列,故B错误;同理也排除D;
,n∈N*,但{an}不是等比数列,故B错误;同理也排除D;对于C,∵am•an=2m+n,m,n∈N*,
∴
 =
= =2,即
=2,即 =2,
=2,∴{an}为等比数列,故C正确.
故选C.
点评:本题考查等比数列的概念与性质,考查举例排除法的应用,考查分析问题与解决问题的能力,属于中档题.

练习册系列答案
相关题目