题目内容
设z∈C,求满足z+ ∈R且|z-2|=2的复数z.
∈R且|z-2|=2的复数z.
 ∈R且|z-2|=2的复数z.
∈R且|z-2|=2的复数z.z=4或z=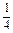 ±
±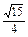 i
i
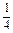 ±
±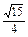 i
i 方法一 设z="a+bi" (a,b∈R),
则z+ =a+bi+
=a+bi+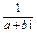 =a+bi+
=a+bi+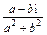
=a+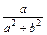 +
+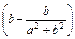 i∈R.
i∈R.
∴b=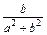 .∴b=0或a2+b2=1.
.∴b=0或a2+b2=1.
当b=0时,z=a,∴|a-2|=2,∴a=0或a=4.
a=0不合题意舍去,∴z=4.
当b≠0时,a2+b2="1. " ①
又∵|z-2|=2,∴(a-2)2+b2="4. " ②
由①②解得a=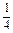 ,b=±
,b=±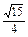 ,∴z=
,∴z=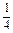 ±
±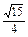 i.
i.
综上可知,z=4或z=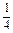 ±
±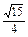 i.
i.
方法二 ∵z+ ∈R,∴z+
∈R,∴z+ =
=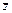 +
+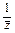 ,
,
∴(z-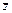 )-
)-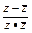 =0,(z-
=0,(z-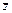 )·
)·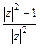 =0,
=0,
∴z=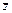 或|z|=1.下同方法一.
或|z|=1.下同方法一.
则z+
 =a+bi+
=a+bi+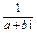 =a+bi+
=a+bi+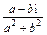
=a+
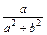 +
+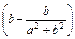 i∈R.
i∈R.∴b=
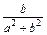 .∴b=0或a2+b2=1.
.∴b=0或a2+b2=1.当b=0时,z=a,∴|a-2|=2,∴a=0或a=4.
a=0不合题意舍去,∴z=4.
当b≠0时,a2+b2="1. " ①
又∵|z-2|=2,∴(a-2)2+b2="4. " ②
由①②解得a=
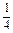 ,b=±
,b=±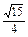 ,∴z=
,∴z=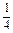 ±
±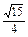 i.
i.综上可知,z=4或z=
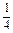 ±
±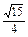 i.
i.方法二 ∵z+
 ∈R,∴z+
∈R,∴z+ =
=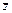 +
+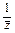 ,
,∴(z-
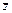 )-
)-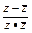 =0,(z-
=0,(z-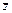 )·
)·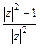 =0,
=0,∴z=
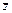 或|z|=1.下同方法一.
或|z|=1.下同方法一.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
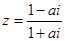 为纯虚数,则实数a等于 ( )
为纯虚数,则实数a等于 ( )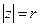 ,求
,求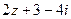 对应的点的轨迹方程.
对应的点的轨迹方程.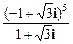 的值是
的值是
 i
i ( ).
( ).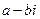 与
与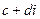 的积是实数的充要条件是 ( )
的积是实数的充要条件是 ( )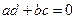



 ,
, ,求满足
,求满足 的复数
的复数 .
.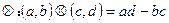 ,则满足
,则满足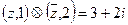 的复数z=________。
的复数z=________。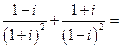 ______________。
______________。