题目内容
如图,在矩形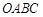 内:记抛物线
内:记抛物线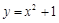 与直线
与直线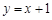 围成的区域为
围成的区域为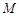 (图中阴影部分).随机往矩形
(图中阴影部分).随机往矩形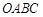 内投一点
内投一点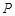 ,则点
,则点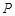 落在区域
落在区域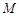 内的概率是( )
内的概率是( )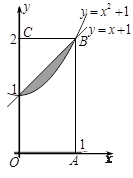
A.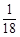 | B.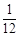 | C.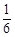 | D.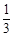 |
B
解析试题分析:根据定积分知识可得阴影部分面积 ,点
,点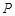 落在区域
落在区域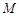 内的概率为关于面积的几何概型,所以由几何概型的概率计算公式得
内的概率为关于面积的几何概型,所以由几何概型的概率计算公式得 ,故选B.
,故选B.
考点:几何概型 定积分

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
曲线
 在x=2处切线方程的斜率是( )
在x=2处切线方程的斜率是( )
| A. 4 | B. 2 | C. 1 | D. |
若 在区间
在区间 上有极值点,则实数
上有极值点,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知

 ,则S1,S2,S3的大小关系为( )
,则S1,S2,S3的大小关系为( )
| A.S1<S2<S3 | B.S2<S1<S3 | C.S2<S3<S1 | D.. S3<S2<S1 |
函数y=1+3x-x3有 ( ).
| A.极小值-1,极大值1 | B.极小值-2,极大值3 |
| C.极小值-2,极大值2 | D.极小值-1,极大值3 |
函数y=(3-x2)ex的单调递增区间是( )
| A.(-∞,0) |
| B.(0,+∞) |
| C.(-∞,-3)和(1,+∞) |
| D.(-3,1) |
已知e为自然对数的底数,则函数y=xex的单调递增区间是( )
| A.[-1,+∞) | B.(-∞,-1] |
| C.[1,+∞) | D.(-∞,1] |
设函数f(x)=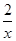 +ln x,则( ).
+ln x,则( ).
A.x= 为f(x)的极大值点 为f(x)的极大值点 | B.x= 为f(x)的极小值点 为f(x)的极小值点 |
| C.x=2为f(x)的极大值点 | D.x=2为f(x)的极小值点 |
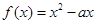 的图像在点A(l,f(1))处的切线l与直线x十3y+2=0垂直,若数列
的图像在点A(l,f(1))处的切线l与直线x十3y+2=0垂直,若数列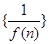 的前n项和为
的前n项和为 ,则S2013的值为 ( )
,则S2013的值为 ( )


