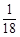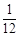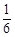题目内容
函数y=(3-x2)ex的单调递增区间是( )
| A.(-∞,0) |
| B.(0,+∞) |
| C.(-∞,-3)和(1,+∞) |
| D.(-3,1) |
D
解析

练习册系列答案
相关题目
设函数f(x)=xex,则( )
| A.x=1为f(x)的极大值点 | B.x=1为f(x)的极小值点 |
| C.x=-1为f(x)的极大值点 | D.x=-1为f(x)的极小值点 |
若函数f(x)=ax4+bx2+c满足f′(1)=2,则f′(-1)等于( )
| A.-1 | B.- 2 | C.2 | D.0 |
已知函数f(x)的导函数为f′(x),且满足f(x)=2xf′(e)+ln x,则f′(e)=( )
| A.1 | B.-1 | C.-e-1 | D.-e |
若0<x< ,则4x与3sin2x的大小关系是( )
,则4x与3sin2x的大小关系是( )
| A.4x>3sin2x | B.4x<3sin2x |
| C.4x=3sin2x | D.与x的取值有关 |
如图,函数y=-x2+2x+1与y=1相交形成一个闭合图形(图中的阴影部分),则该闭合图形的面积是( )
| A.1 | B. | C. | D.2 |
函数y=2x3+1的图象与函数y=3x2-b的图象有三个不相同的交点,则实数b的取值范围是( )
| A.(-2,-1) | B.(-1,0) |
| C.(0,1) | D.(1,2) |
设f(x)在(a,b)内可导,则f′(x)<0是f(x)在(a,b)内单调递减的( )
| A.充分不必要条件 |
| B.必要不充分条件 |
| C.充要条件 |
| D.既不充分也不必要条件 |
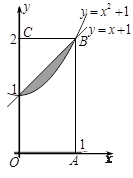
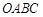 内:记抛物线
内:记抛物线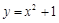 与直线
与直线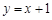 围成的区域为
围成的区域为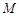 (图中阴影部分).随机往矩形
(图中阴影部分).随机往矩形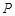 ,则点
,则点