题目内容
(本题满分10分)已知函数 ,
,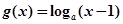 ,其中
,其中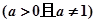 ,设
,设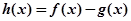 .
.
(Ⅰ) 判断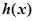 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(Ⅱ)当 时,判断并证明函数
时,判断并证明函数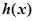 的单调性;
的单调性;
(Ⅲ) 若 ,且对于区间[3,4]上的每一个x的值,不等式
,且对于区间[3,4]上的每一个x的值,不等式
 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
【答案】
解:(1) ,
,
所以h(x)为奇函数.
(2)因为
记u(x)=1+ ,
,

所以u
又因为 函数
函数 为减函数,所以
为减函数,所以

 在
在 上为增函数.
上为增函数.
(3)由 ,得
,得 ,
,
设 .
.
由(2)中的证明及函数单调性的判定方法,易证明
 在[3,4]上为增函数, 此处从略 .
在[3,4]上为增函数, 此处从略 .
那么要使  >m对x∈[3,4]恒成立,
>m对x∈[3,4]恒成立,
只需m< .
.
所以
【解析】略

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 .
.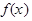 的单调区间;
的单调区间; 且
且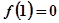 .
. 是偶函数,求函数
是偶函数,求函数 上的最大值和最小值;
上的最大值和最小值; 的取值范围.
的取值范围. ∩
∩ =m,a∥
=m,a∥