题目内容
ABCD是边长为a的正方形，作MN∥AB，分别交AD、BC于点M、N（如图甲）.沿MN折成直二面角AMNC（如图乙），求MN在什么位置时，异面直线AC和MN间距离最大？并求出此最大值.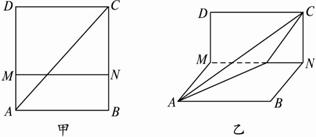
解析：连结AD，由MN∥CD，可证MN∥平面ACD，∴MN与AC的距离等于MN与平面ACD的距离，也就等于点M到平面ACD的距离.由MN⊥平面AMD，得CD⊥平面AMD.∴平面ACD⊥平面AMD.作MH⊥AD于H，可证MH⊥平面ACD.?
∴MH是点M到平面ACD的距离.?
在Rt△AMD中，?
MH=
≤
?
=
?
≤
.?
∴当AM=MD=
,即M是AD中点时，MH最大，最大值为
.
练习册系列答案
阅读快车系列答案
相关题目
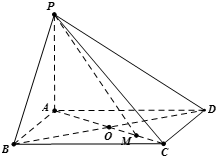已知四棱锥中，PA⊥平面ABCD，底面ABCD是边长为a的菱形，∠BAD=120°，PA=b．
（2012•顺河区一模）选做题：几何证明选讲
如图所示，ABCD是边长为a的正方形，△PBA是以角B为直角的等腰三角形，H为BD上一点，且AH⊥平面PDB．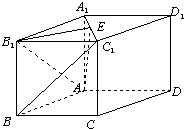
如图，直四棱柱ABCD-A1B1C1D1中，底面ABCD是边长为a的菱形，且∠ABC=60°，侧棱长为
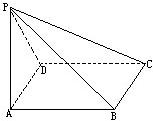四棱锥P-ABCD的底面ABCD是边长为a的正方形，侧棱PA=a，