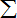题目内容
以一个平行四边形的4个顶点为起点和终点作向量，其中互不相等的向量共有
- A.4个
- B.6个
- C.8个
- D.12个
C
分析：根据题意，以一个平行四边形的4个顶点为起点和终点作向量，因为向量是有方向的，是排列问题；计算可得其数目，再排除其中相等的向量，计算可得答案．
解答：
解：根据题意，以一个平行四边形的4个顶点为起点和终点作向量，
共有A42=12个；
而其中相等的为平行四边形的对边上的向量，共四组；
故其中互不相等的向量共有12-4=8个；
故选C．
点评：本题考查排列的应用，注意向量具有方向，是排列问题；若是线段或直线，则是组合问题．
分析：根据题意，以一个平行四边形的4个顶点为起点和终点作向量，因为向量是有方向的，是排列问题；计算可得其数目，再排除其中相等的向量，计算可得答案．
解答：
解：根据题意，以一个平行四边形的4个顶点为起点和终点作向量，共有A42=12个；
而其中相等的为平行四边形的对边上的向量，共四组；
故其中互不相等的向量共有12-4=8个；
故选C．
点评：本题考查排列的应用，注意向量具有方向，是排列问题；若是线段或直线，则是组合问题．
练习册系列答案
同步练习河南大学出版社系列答案
相关题目
