题目内容
设命题p：“x≠1”是“x3≠x”的充分不必要条件；命题q：
=
=
是不等式a1x2+b1x+c1＞0和a2x2+b2x+c2＞0同解的充要条件，则以下是真命题的是（ ）
| a1 |
| a2 |
| b1 |
| b2 |
| c1 |
| c2 |
分析：通过逆否命题的真假一致判断出命题p为假命题，通过举反例判断出命题q为假命题，利用复合命题的真值表得到选项．
解答：解：对于命题p，因为“x3=x”是“x=1”必要不充分条件，
所以：“x≠1”是“x3≠x”的必要不充分条件；
故命题p是假命题；所以￢p为真命题，
对于命题q，举反例a1=b1=c1=1，a2=b2=c2=-1，满足
=
=
，
但此时等式a1x2+b1x+c1＞0和a2x2+b2x+c2＞0不同解，
所以命题q是假命题；所以￢q为真命题，
所以￢p或q为真命题，
故选D．
所以：“x≠1”是“x3≠x”的必要不充分条件；
故命题p是假命题；所以￢p为真命题，
对于命题q，举反例a1=b1=c1=1，a2=b2=c2=-1，满足
| a1 |
| a2 |
| b1 |
| b2 |
| c1 |
| c2 |
但此时等式a1x2+b1x+c1＞0和a2x2+b2x+c2＞0不同解，
所以命题q是假命题；所以￢q为真命题，
所以￢p或q为真命题，
故选D．
点评：本题考查判断复合命题的真假，应该先判断出构成复合命题的简单命题的真假，然后根据复合命题的真值表进行判断，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
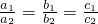是不等式a1x2+b1x+c1＞0和a2x2+b2x+c2＞0同解的充要条件，则以下是真命题的是