题目内容
在△ABC中,内角A,B,C的对边分别为a,b,c.已知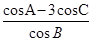 =
=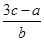 .
.
(1)求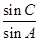 的值;
的值;
(2)若B为钝角,b=10,求a的取值范围.
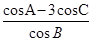 =
=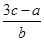 .
.(1)求
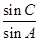 的值;
的值;(2)若B为钝角,b=10,求a的取值范围.
(1)3 (2)(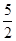 ,
,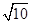 )
)
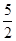 ,
,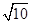 )
)解:(1)由正弦定理,设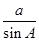 =
=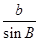 =
=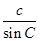 =k,
=k,
则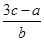 =
=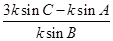 =
=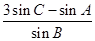 ,
,
所以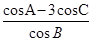 =
=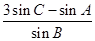 .
.
即(cosA-3cosC)sinB=(3sinC-sinA)cosB,
化简可得sin(A+B)=3sin(B+C).
又A+B+C=π,
所以sinC=3sinA,
因此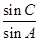 =3.
=3.
(2)由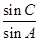 =3得c=3a.
=3得c=3a.
由题意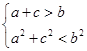 ,即
,即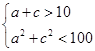 ,
,
所以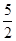 <a<
<a<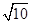 .故a的取值范围为(
.故a的取值范围为(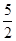 ,
,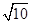 ).
).
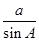 =
=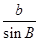 =
=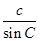 =k,
=k,则
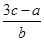 =
=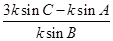 =
=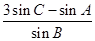 ,
,所以
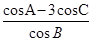 =
=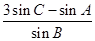 .
.即(cosA-3cosC)sinB=(3sinC-sinA)cosB,
化简可得sin(A+B)=3sin(B+C).
又A+B+C=π,
所以sinC=3sinA,
因此
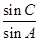 =3.
=3.(2)由
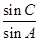 =3得c=3a.
=3得c=3a.由题意
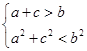 ,即
,即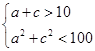 ,
,所以
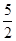 <a<
<a<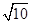 .故a的取值范围为(
.故a的取值范围为(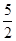 ,
,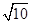 ).
).
练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
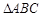 中,角
中,角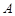 、
、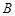 、
、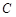 所对的边分别为
所对的边分别为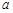 、
、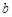 、
、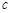 ,满足
,满足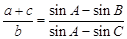 .
.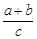 的取值范围.
的取值范围.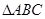 中,角
中,角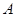 、
、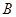 、
、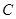 所对的边分别为
所对的边分别为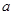 、
、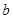 、
、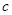 ,已知
,已知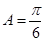 ,
,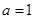 ,
,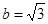 ,则
,则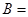 ________.
________.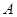 、
、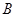 、
、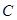 分别为
分别为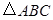 的三边
的三边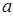 、
、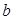 、
、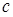 所对的角,向量
所对的角,向量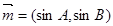 ,
,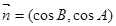 ,且
,且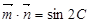 .
.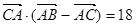 ,求边
,求边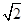
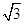
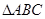 三个内角
三个内角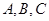 满足
满足 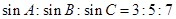 ,则此三角形内角的最大值为 .
,则此三角形内角的最大值为 .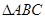 中,角
中,角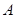 、
、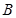 、
、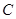 的对边分别为
的对边分别为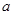 、
、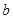 、
、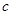 ,且
,且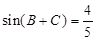 ,
,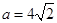 ,
,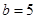 .
.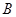 与边
与边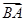 在
在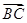 方向上的投影.
方向上的投影.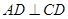 ,
,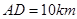 ,
,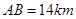 ,
,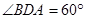 ,
,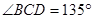 ,求两景点B与C的距离.
,求两景点B与C的距离.
 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为 ,若
,若 ( )
( )


