题目内容
【题目】已知![]() .
.
(1)当![]() 时,求
时,求![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析: (1)求出f(x)的导数,可得切线的斜率,由斜截式方程即可得到所求切线的方程;
(2)由题意可得存在x0∈[0,+∞),使得![]() ,设
,设![]() ,两次求导,判断单调性,对a讨论,分
,两次求导,判断单调性,对a讨论,分![]() 和
和![]() 时,通过构造函数和求导,得到单调区间,可得最值,即可得到所求a的范围.
时,通过构造函数和求导,得到单调区间,可得最值,即可得到所求a的范围.
试题解析:(1)![]() 时,
时, ![]() ,
, ![]()
![]() ,
, ![]() ,
,
所以![]() 在
在![]() 处的切线方程为
处的切线方程为![]()
(2)存在![]() ,
, ![]() ,
,
即: ![]() 在
在![]() 时有解;
时有解;
设![]() ,
, ![]()
令![]() ,
, ![]()
所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]()
1°当![]() 时,
时, ![]() ,∴
,∴![]() 在
在![]() 单调增,
单调增,
所以![]() ,所以
,所以![]()
2°当![]() 时,
时, ![]()
设![]() ,
,
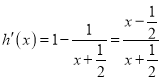
令![]() ,
, ![]()
所以![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增
单调递增
所以![]() ,所以
,所以![]()
所以![]()
![]()
设![]() ,
, ![]() ,
,
令![]() ,
, ![]()
所以![]() 在
在![]() 上单调递增,
上单调递增,
所以![]()
所以![]() 在
在![]() 单调递增,∴
单调递增,∴![]() ,
,
所以![]() ,
,
所以![]()
所以,当![]() 时,
时, ![]() 恒成立,不合题意
恒成立,不合题意
综上,实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】对一批共50件的某电器进行分类检测,其重量(克)统计如下:
质量段 | [80,85) | [85,90) | [90,95) | [95,100] |
件数 | 5 | a | 15 | b |
规定重量在82克及以下的为“A”型,重量在85克及以上的为“B”型,已知该批电器有“A“型2件
(1)从该批电器中任选1件,求其为“B”型的概率;
(2)从重量在[80,85)的5件电器中,任选2件,求其中恰有1件为“A”型的概率.