题目内容
已知焦点在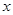 轴上椭圆的长轴的端点分别为
轴上椭圆的长轴的端点分别为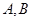 ,
,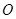 为椭圆的中心,
为椭圆的中心,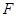 为右焦点,且
为右焦点,且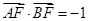 ,离心率
,离心率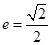 。
。
(Ⅰ)求椭圆的标准方程;
(Ⅱ)记椭圆的上顶点为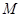 ,直线
,直线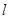 交椭圆于
交椭圆于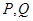 两点,问:是否存在直线
两点,问:是否存在直线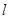 ,使点
,使点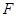 恰好为
恰好为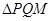 的垂心?若存在,求出直线
的垂心?若存在,求出直线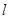 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。
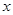 轴上椭圆的长轴的端点分别为
轴上椭圆的长轴的端点分别为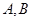 ,
,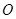 为椭圆的中心,
为椭圆的中心,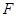 为右焦点,且
为右焦点,且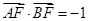 ,离心率
,离心率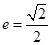 。
。(Ⅰ)求椭圆的标准方程;
(Ⅱ)记椭圆的上顶点为
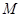 ,直线
,直线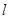 交椭圆于
交椭圆于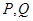 两点,问:是否存在直线
两点,问:是否存在直线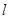 ,使点
,使点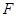 恰好为
恰好为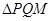 的垂心?若存在,求出直线
的垂心?若存在,求出直线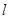 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。(Ⅰ)略
(Ⅱ)假设存在直线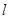 交椭圆与点
交椭圆与点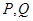 两点,且
两点,且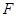 恰为
恰为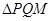 的垂心,设
的垂心,设 ,
, ,因为
,因为 ,故
,故 。于是设直线
。于是设直线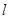 为
为 ,由
,由 得
得
所以: ,
,


又

即:
由韦达定理得:
解得 或
或 (舍去)
(舍去)
经检验 符合条件,故直线
符合条件,故直线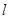 的方程为
的方程为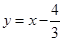 。
。

(Ⅱ)假设存在直线
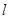 交椭圆与点
交椭圆与点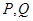 两点,且
两点,且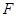 恰为
恰为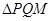 的垂心,设
的垂心,设 ,
, ,因为
,因为 ,故
,故 。于是设直线
。于是设直线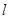 为
为 ,由
,由 得
得
所以:
 ,
,


又


即:

由韦达定理得:

解得
 或
或 (舍去)
(舍去)经检验
 符合条件,故直线
符合条件,故直线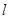 的方程为
的方程为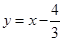 。
。略

练习册系列答案
相关题目
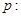 “椭圆
“椭圆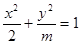 的焦点在
的焦点在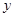 轴上”;
轴上”;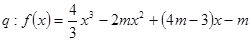 在
在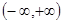 上单调递增,若“
上单调递增,若“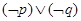 ”为假,求
”为假,求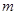 的取值范围.
的取值范围.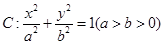 的离心率为
的离心率为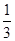 ,椭圆上的点到右焦点F的最近距离为2,若椭圆C与x轴交于A、B两点,M是椭圆C上异于A、B的任意一点,直线MA交直线
,椭圆上的点到右焦点F的最近距离为2,若椭圆C与x轴交于A、B两点,M是椭圆C上异于A、B的任意一点,直线MA交直线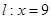 于G点,直线MB交直线
于G点,直线MB交直线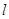 于H点。
于H点。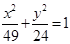 共焦点,且以
共焦点,且以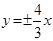 为渐近线,求双曲线方程.
为渐近线,求双曲线方程.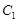 :
: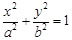 (
(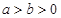 )的离心率为
)的离心率为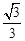 ,直线
,直线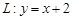 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆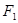 ,右焦点为
,右焦点为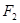 ,直线
,直线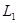 过点
过点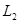 垂直
垂直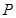 ,线段
,线段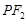 的垂直平分线交
的垂直平分线交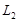 于点
于点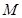 .
.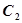 的方程;
的方程;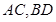 为点
为点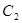 的过点
的过点 面积的最小值.
面积的最小值.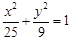 ,F是右焦点,
,F是右焦点,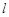 是过点F的一条直线(不与
是过点F的一条直线(不与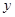 轴平行),交椭圆于A、B两点,
轴平行),交椭圆于A、B两点, 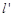 是AB的中垂线,交椭圆的长轴于一点D,则
是AB的中垂线,交椭圆的长轴于一点D,则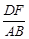 的值是 .
的值是 .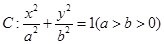 恒过定点
恒过定点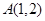 ,则椭圆的中心到准线的距离的
,则椭圆的中心到准线的距离的 的焦点为
的焦点为 ,点p在椭圆上,若
,点p在椭圆上,若 ,则
,则
 的大小为
的大小为 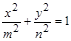 ,
,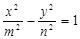 ,
,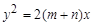 ,(其中
,(其中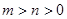 )的离心率分别为
)的离心率分别为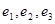 ,则( ).
,则( ).


 大小不确定
大小不确定