题目内容
已知Ω={（x，y）|
}，直线y=mx+2m和曲线y=
有两个不同的交点，它们围成的平面区域为M，向区域Ω上随机投一点A，点A落在区域M内的概率为P（M），若P（M）∈[
，1]，则实数m的取值范围
- A.[
，1] - B.[0，
] - C.[，1]
- D.[0，1]
D
分析：画出图形，不难发现直线恒过定点（-2，0），结合概率范围可知直线与圆的关系，
直线以（-2，0）点为中心顺时针旋转至与x轴重合，从而确定直线的斜率范围．
解答：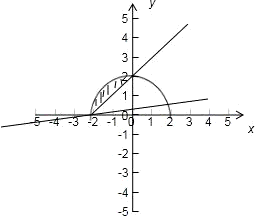
解：画出图形，不难发现直线恒过定点（-2，0），
圆是上半圆，直线过（-2，0），（0，2）时，
它们围成的平面区域为M，向区域Ω上随机投一点A，
点A落在区域M内的概率为P（M），此时P（M）=，
当直线与x轴重合时，P（M）=1；
直线的斜率范围是[0，1]．
故选D．
点评：本题考查直线与圆的方程的应用，几何概型，直线系，数形结合的数学思想，是好题，难度较大．
分析：画出图形，不难发现直线恒过定点（-2，0），结合概率范围可知直线与圆的关系，
直线以（-2，0）点为中心顺时针旋转至与x轴重合，从而确定直线的斜率范围．
解答：
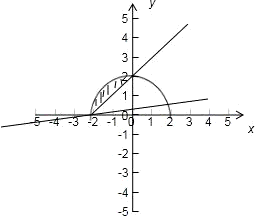解：画出图形，不难发现直线恒过定点（-2，0），圆是上半圆，直线过（-2，0），（0，2）时，
它们围成的平面区域为M，向区域Ω上随机投一点A，
点A落在区域M内的概率为P（M），此时P（M）=
，当直线与x轴重合时，P（M）=1；
直线的斜率范围是[0，1]．
故选D．
点评：本题考查直线与圆的方程的应用，几何概型，直线系，数形结合的数学思想，是好题，难度较大．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
已知A={（x，y）||x-a|+|y-1|≤1}，B={（x，y）|（x-1）2+（y-1）2≤1}，若集合A∩B≠φ，则实数a的取值范围是（ ）
| A、[-1，3] | ||||
B、[-1-
| ||||
| C、[-3，1] | ||||
| D、[0，2] |