题目内容
设数列![]() 满足
满足![]() ,若
,若![]() 是等差数列,
是等差数列,![]() 是等比数列.
是等比数列.
(1)分别求出数列![]() 的通项公式;
的通项公式;
(2)是否存在![]() ,使
,使![]() ,若存在,求满足条件的所有
,若存在,求满足条件的所有![]() 值;若不存在,请说明理由.
值;若不存在,请说明理由.
解:(1)![]() 由
由![]() 成等差数列知其公差为1,
成等差数列知其公差为1,
故![]() ………………1分
………………1分
![]() 由
由![]() 等比数列知,其公比为
等比数列知,其公比为![]() ,
,
故![]() ……2
……2
![]() =
=
![]() +6=
+6=![]() =
=![]() ……4分
……4分
![]()
 ………………………………………………6分
………………………………………………6分
(3)假设![]() 存在,使
存在,使![]()
则![]() 即
即![]() …………
…………
∵![]() 与
与![]() 是相邻整数
是相邻整数
∴![]() ,这与
,这与![]() 矛盾,所以满足条件的
矛盾,所以满足条件的![]() 不存在
不存在

练习册系列答案
相关题目
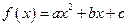 满足条件:①
满足条件:① 是
是 的两个零点;②
的两个零点;② 的最小值为
的最小值为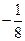
 的前
的前 项积为
项积为 ,且
,且 ,
, ,求数列
,求数列
 时,若
时,若 是
是 与
与 的等差中项,试问数列
的等差中项,试问数列 中
中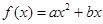 满足条件:
满足条件: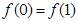 ;②
;②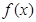 的最小值为
的最小值为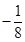 。
。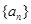 的前
的前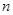 项积为
项积为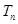 ,且
,且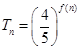 ,求数列
,求数列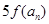 是
是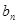 与
与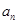 的等差中项,试问数列
的等差中项,试问数列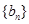 中第几项的值最小?求出这个最小值。
中第几项的值最小?求出这个最小值。