题目内容
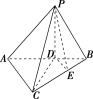
【题目】如图，已知圆锥的顶点为S，底面圆O的两条直径分别为AB和CD，且AB⊥CD，若平面
平面
．现有以下四个结论：
①AD∥平面SBC；
②
；
③若E是底面圆周上的动点，则△SAE的最大面积等于△SAB的面积；
④
与平面SCD所成的角为45°．
其中正确结论的序号是__________．
【答案】①②④
【解析】
利用线面平行判定定理说明①的正误；利用线面平行性质定理说明②的正误；由
，讨论∠ASB的锐钝可说明③的正误；利用
与平面SCD所成的角等于AD与平面SCD所成的角可判断④的正误.
由AB和CD是圆O得直径及AB⊥CD，得四边形ABCD为正方形，则AD∥BC，
从而AD∥平面SBC，则①正确；又因为
平面SAD，且
平面
，所以
，则②正确；因为，当∠ASB为钝角时，
；
当∠ASB为锐角或直角时，
，则③不正确；由，得与平面SCD所成的角等于AD与平面SCD所成的角，即为∠ADO，又因为∠ADO=45°，故④正确.
故答案为：①②④
新课标阶梯阅读训练系列答案
【题目】某公司为了解某产品的获利情况，将今年1至7月份的销售收入
（单位：万元）与纯利润
（单位：万元）的数据进行整理后，得到如下表格：
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售收入 | 13 | 13.5 | 13.8 | 14 | 14.2 | 14.5 | 15 |
纯利润 | 3.2 | 3.8 | 4 | 4.2 | 4.5 | 5 | 5.5 |
该公司先从这7组数据中选取5组数据求纯利润关于销售收入的线性回归方程，再用剩下的2组数据进行检验.假设选取的是2月至6月的数据.
（1）求纯利润关于销售收入
（2）若由线性回归方程得到的估计数据与检验数据的误差均不超过0.1万元，则认为得到的线性回归方程是理想的.试问该公司所得线性回归方程是否理想？
参考公式：
，
，
，
；参考数据：
.
【题目】某地区不同身高
的未成年男性的体重平均值
如下表：
身高x（cm） | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 |
体重y(kg) | 6.13 | 7.90 | 9.99 | 12.15 | 15.02 | 17.50 | 20.92 | 26.86 | 31.11 |
已知
与
之间存在很强的线性相关性，
（Ⅰ）据此建立
与之间的回归方程；
（Ⅱ）若体重超过相同身高男性体重平均值的
倍为偏胖，低于
倍为偏瘦，那么这个地区一名身高
体重为
的在校男生的体重是否正常？
参考数据：
附：对于一组数据
，其回归直线
中的斜率和截距的最小二乘估计分别为