题目内容
(12分)已知等差数列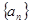 的公差大于0,且
的公差大于0,且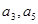 是方程
是方程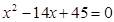 的两根,数列
的两根,数列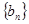 的前
的前 项的和为
项的和为 ,且
,且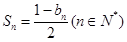 .
.
(1)求数列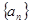 ,
,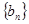 的通项公式;
的通项公式;
(2)记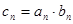 ,求证:
,求证: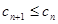 ;
;
(3)求数列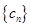 的前
的前 项和
项和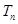 .
.
【答案】
(1)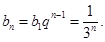 (2)见解析;(3)
(2)见解析;(3)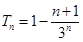 。
。
【解析】
试题分析:(1)由已知可得,a3+a5= 14, a3•a5=45且a5>a3,联立方程解得a5,a3,进一步求出数列{an}通项,数列{bn}中,利用递推公式bn= sn-sn-1,n≥2
s1 ,n=1
(2)把(1)中求得的an和bn代入cn=anbn,求得cn,进而可求得cn+1-cn求得结果小于等于0,原式得证.
(3)用错位相减求数列{cn}的前n和
解:(1)∵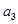 ,
,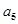 是方程
是方程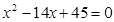 的两根,且数列
的两根,且数列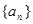 的公差
的公差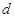 >0,
>0,
∴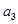 =5,
=5,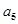 =9,公差
=9,公差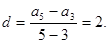 ∴
∴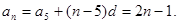 ………3分
………3分
又当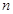 =1时,有
=1时,有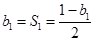
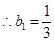
当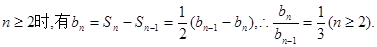
∴数列{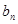 }是首项
}是首项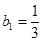 ,公比
,公比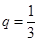 等比数列,
等比数列,
∴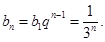 …………4分
…………4分
(2)由(1)知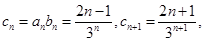 …………6分
…………6分
∴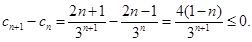
∴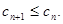 …………………………8分
…………………………8分
(3)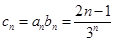 ,设数列
,设数列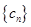 的前
的前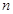 项和为
项和为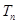 ,
,
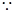
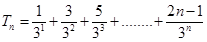 (1)
(1)

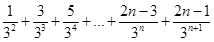 (2)
………………10分
(2)
………………10分
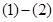 得:
得:
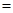

化简得: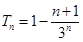 ………………………12分
………………………12分
考点:本试题主要考查了等差数列的通项公式和等比数列的通项公式,属基础题.
点评:解决该试题的关键是利用递推公式求通项,体现了数学中的转化思想;一般的,若数列{an}为等差数列,{bn}为等比数列,求数列{an•bn}的前n和可采用错位相减法.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
 的公差为
的公差为 ,前
,前 项和为
项和为 ,且满足
,且满足 ,
, 表示不等式组
表示不等式组 ,并在给定的坐标系中画出不等式组表示的平面区域;
,并在给定的坐标系中画出不等式组表示的平面区域; 的最大值,并指出此时数列
的最大值,并指出此时数列 [
[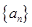 的公差
的公差 ,若
,若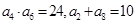 ,则该数列的前
,则该数列的前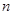 项和
项和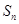 的最大值是( )
的最大值是( )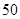 B.
B.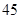 C.
C.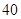 D.
D.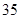
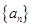 的公差
的公差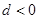 ,前
,前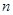 项和
项和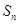 满足:
满足: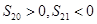 ,那么数列
,那么数列 中最大的值是(
)
中最大的值是(
)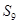 B.
B.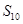 C.
C.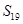 D.
D.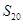
 的公差
的公差 ,若
,若 ,则该数列的前
,则该数列的前 项和
项和 的最大值为( )
的最大值为( ) B.
B. C.
C. D.
D.
 的公差为负数,且
的公差为负数,且 ,若
,若 经重新排列后依次可成等比数列,求⑴数列
经重新排列后依次可成等比数列,求⑴数列 ;⑵数列
;⑵数列 项和
项和 的最大值。
的最大值。