题目内容
已知| OA |
| x |
| 3 |
| 3 |
| x |
| 3 |
| OB |
| x |
| 3 |
| x |
| 3 |
| OA |
| OB |
（Ⅰ）求函数f（x）的解析式及最小正周期；
（Ⅱ）若x∈（0，
| π |
| 3 |
分析：（Ⅰ）欲求函数的解析式，只要运用向量积的点坐标运算公式计算得到
•
的结果．欲求函数的最小正周期，运用最小正周期的计算公式T= |
|即可．
（Ⅱ）要求函数值域，只要根据定义域及三角函数的值域的求法即可．
| OA |
| OB |
| 2π |
| w |
（Ⅱ）要求函数值域，只要根据定义域及三角函数的值域的求法即可．
解答：解：（1）f(x)=
•
=sin
cos
+
cos2
（2分）
=f(x)=
sin
+
（4分）
=sin(
+
)+
（5分）T=3π（7分）
（Ⅱ）由0＜x≤
，
＜
+
≤
则
＜sin(
+
) ≤1（10分）
∴函数f（x）的值域为(
，1+
]（12分）
| OA |
| OB |
| x |
| 3 |
| x |
| 3 |
| 3 |
| x |
| 3 |
=f(x)=
| 1 |
| 2 |
| 2x |
| 3 |
| 3 |
1+cos
| ||
| 2 |
=sin(
| 2x |
| 3 |
| π |
| 3 |
| ||
| 2 |
（Ⅱ）由0＜x≤
| π |
| 3 |
| π |
| 3 |
| 2x |
| 3 |
| π |
| 3 |
| 5π |
| 9 |
则
| ||
| 2 |
| 2x |
| 3 |
| π |
| 3 |
∴函数f（x）的值域为(
| 3 |
| ||
| 2 |
点评：本题考查平面向量数量积的运算，三角函数的周期性及其求法，同时还考查了三角函数的最值的求法．
练习册系列答案
相关题目
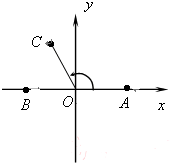在如图所示的平面直角坐标系中，已知点．A（1，0）和点B（-1，0），