题目内容
(本小题满分12分)
已知函数 .
.
(1)求 的值;
的值;
(2)求函数 的最小正周期及单调递增区间.
的最小正周期及单调递增区间.
(1) ;(2)
;(2) ,
,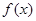 的单调递增区间为
的单调递增区间为 .
.
解析试题分析:思路一:(1)直接将 代入函数式,应用三角函数诱导公式计算.
代入函数式,应用三角函数诱导公式计算.
(2)应用和差倍半的三角函数公式,将函数化简 .
.
得到 .
.
由 ,
,
解得 .
.
思路二:先应用和差倍半的三角函数公式化简函数

(1)将 代入函数式计算;
代入函数式计算;
(2)
由 ,
,
解得 .
.
试题解析:解法一:(1)


(2)因为

 .
.
所以 .
.
由 ,
,
得 ,
,
所以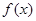 的单调递增区间为
的单调递增区间为 .
.
解法二:
因为


(1)
(2)
由 ,
,
得 ,
,
所以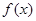 的单调递增区间为
的单调递增区间为 .
.
考点:和差倍半的三角函数公式,三角函数诱导公式,三角函数的图象和性质.

练习册系列答案
相关题目
 ,且
,且 的图象的一个对称中心到最近的对称轴的距离为
的图象的一个对称中心到最近的对称轴的距离为 ,(1)求
,(1)求 的值;(2)求
的值;(2)求 在区间
在区间 上的最大值和最小值.
上的最大值和最小值. ,
, .
. 是函数
是函数 的一个零点,求
的一个零点,求 的值;
的值; 的单调递增区间.
的单调递增区间. (sin2x-cos2x)-2sinxcosx.
(sin2x-cos2x)-2sinxcosx. ,
, ,
, ,且
,且 .
. 的值;
的值; ,
, ,求
,求 .
. .
. ,
, ,且C为锐角,求
,且C为锐角,求 .
. )+2a+b,当x∈[0,
)+2a+b,当x∈[0, ]时,-5≤f(x)≤1.
]时,-5≤f(x)≤1. ,
, cos(
cos( cos(-α)=-
cos(-α)=-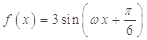 ,
,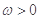 ,
,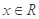 ,且以
,且以 为最小正周期.
为最小正周期. ;
;
 的解析式;
的解析式;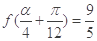 ,求
,求 的值.
的值.