题目内容
已知函数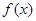 是
是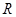 上的偶函数,且满足
上的偶函数,且满足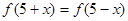 ,在[0,5]上有且只有
,在[0,5]上有且只有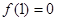 ,则
,则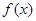 在[–2013,2013]上的零点个数为
在[–2013,2013]上的零点个数为
| A.808 | B.806 | C.805 | D.804 |
B
解析试题分析:因为函数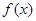 是
是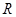 上的偶函数,在[0,5]上有且只有一个零点,所以在
上的偶函数,在[0,5]上有且只有一个零点,所以在 上也只有一个零点,而
上也只有一个零点,而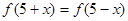 说明函数以x=5为对称轴,所以周期是10,每个周期上有两个零点,所以
说明函数以x=5为对称轴,所以周期是10,每个周期上有两个零点,所以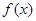 在[–2013,2013]上的零点个数为806.
在[–2013,2013]上的零点个数为806.
考点:本小题主要考查函数的奇偶性,对称性和零点个数问题.
点评:函数的单调性,奇偶性,周期性,对称性是函数的重要性质,经常结合出题,综合考查,要牢固掌握,灵活应用.

练习册系列答案
相关题目
函数 的值域是( )
的值域是( )
A. | B. | C. | D. |
如图是导函数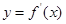 的图象,则下列命题错误的是( )
的图象,则下列命题错误的是( )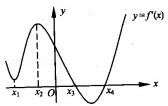
A.导函数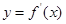 在 在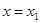 处有极小值 处有极小值 |
B.导函数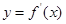 在 在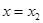 处有极大值 处有极大值 |
C.函数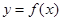 在 在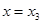 处有极小值 处有极小值 |
D.函数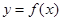 在 在 处有极小值 处有极小值 |
方程 的实根个数是( )
的实根个数是( )
| A.3 | B.2 | C.1 | D.0 |
函数y=x+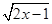 ( )
( )
A.有最小值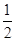 ,无最大值 ,无最大值 |
B.有最大值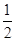 ,无最小值 ,无最小值 |
C.有最小值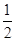 ,最大值2 ,最大值2 |
| D.无最大值,也无最小值 |
设f(x)是定义在R上的奇函数,且当x>0时,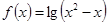 ,则f(-2)=
,则f(-2)=
A.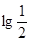 | B.lg2 | C.2lg2 | D.lg6 |
下列函数中,在其定义域内既是奇函数又是减函数的是( )
A.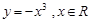 | B. | C. | D.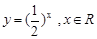 |
设函数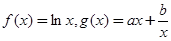 ,它们的图象在
,它们的图象在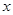 轴上的公共点处有公切线,则当
轴上的公共点处有公切线,则当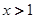 时,
时,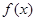 与
与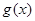 的大小关系是( )
的大小关系是( )
A.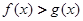 | B.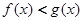 |
C.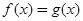 | D.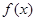 与 与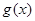 的大小不确定 的大小不确定 |
已知函数 ,
, ,且
,且 ,当
,当 时,
时, 是增函数,设
是增函数,设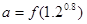 ,
,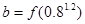 ,
, ,则
,则 、
、 、
、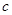 的大小顺序是( )。
的大小顺序是( )。
A. | B.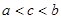 | C. | D. |