Question

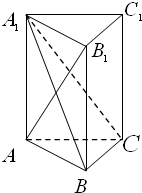如图，在直三棱柱ABC-A₁B₁C₁中，AB⊥AC，且AB=AA₁=1
（1）求证：A₁B⊥B₁C
（2）求点C₁到平面AB₁C的距离；
（3）设二面角A-B₁C-B的大小为θ，求θ的取值范围．

Answer 1

分析：（1）直接根据其为直棱柱以及AB=AA₁=1得到AC⊥A₁B和A₁B⊥AB₁；即可得A₁B⊥B₁C；
（2）先根据A₁C₁∥AC把点C₁到平面AB₁C的距离转化为点A₁到平面AB₁C的距离；再结合第一问的结论即可求出结果；
（3）先建立空间直角坐标系，求出两个半平面的法向量，再代入向量的夹角计算公式结合不等式即可求出答案．

解答：解：（1）因为在直三棱柱ABC-A₁B₁C₁中，AB⊥AC，且AB=AA₁=1
所以：AC⊥AA₁，⇒AC⊥平面AA₁B₁B⇒AC⊥A₁B①；
又AA₁B₁B为正方形⇒A₁B⊥AB₁；②
由①②⇒A₁B⊥平面ACB₁⇒A₁B⊥B₁C．
（2）∵A₁C₁∥AC⇒A₁C₁∥平面ACB₁⇒
所以点C₁到平面AB₁C的距离等于点A₁到平面AB₁C的距离；
由第一问的结论得：A₁B⊥平面ACB₁⇒A₁到平面AB₁C的距离等于：

A1B

2

=

2

2

．
即点C₁到平面AB₁C的距离为：

2

2

．
（3）以AC为X轴，AB为Y轴，AA₁为Z轴建立直角坐标系；设AC=a
则A（0，0，0），B（0，1，0），C（a，0，0）B₁（0，1，0），A₁（1，0，1）．
∴

AB1

=（0，1，1），

AC

=（a，0，0），

B1B

=（0，0，-1），

BC

=（a，-1，0）．
设平面AB₁C的法向量

n

=（x，y，z）
∵

n

•

AB1

=0，

n

•

AC

=0⇒y+z=0，ax=0⇒

n

=（0，1，-1）；
设平面BB₁C的法向量

m

=（e，f，g）．
∵

m

•

B1B

=0，

m

•

BC

=0⇒g=0，ea-f=0⇒

m

=（1，a，0）．
∴0＜cos＜

n

，

m

＞=

a

2 × 1+a2

=

1

2+ 2 a2

＜

1

2

=

2

2

．
∴θ的取值范围：（45°，90°）．

点评：本题主要考查线线垂直的证明以及点到面的距离和二面角的求法．是对立体几何知识的综合考查，属于综合性题目，解决第三问用到了空间向量，直接找二面角的平面角有点麻烦．