题目内容
18.已知关于x的方程169x2-bx+60=0的两根为sinθ,cosθ,$θ∈({\frac{π}{4}\;,\;\;\frac{3π}{4}})$.(1)求实数b的值;
(2)求$\frac{sinθ}{1-cosθ}+\frac{1+cosθ}{sinθ}$的值.
分析 (1)根据题意,利用韦达定理列出关系式,利用完全平方公式及同角三角函数间的基本关系化简求出b的值即可;
(2)由b的值,利用完全平方公式求出sinθ与cosθ的值,原式通分并利用同角三角函数间的基本关系化简,将sinθ与cosθ的值代入计算即可求出值.
解答 解:(1)∵169x2-bx+60=0的两根为sinθ、cosθ,
∴sinθ+cosθ=$\frac{b}{169}$,sinθcosθ=$\frac{60}{169}$>0,
∵$θ∈({\frac{π}{4}\;,\;\;\frac{3π}{4}})$,
∴θ+$\frac{π}{4}$∈($\frac{π}{2}$,π),即sinθ+cosθ=$\sqrt{2}$sin(θ+$\frac{π}{4}$)>0,
∴(sinθ+cosθ)2=sin2θ+cos2θ+2sinθcosθ=1+2×$\frac{60}{169}$=($\frac{b}{169}$)2,
解得:b=±221(负值舍去),则b=221;
(2)∵(sinθ-cosθ)2=sin2θ+cos2θ-2sinθcosθ=1-2×$\frac{60}{169}$=$\frac{49}{169}$,
∴sinθ-cosθ=$\frac{7}{13}$,
∵sinθ+cosθ=$\frac{17}{13}$,
∴sinθ=$\frac{12}{13}$,cosθ=$\frac{5}{13}$,
则原式=$\frac{si{n}^{2}θ+1-co{s}^{2}θ}{sinθ(1-cosθ)}$=$\frac{2sinθ}{1-cosθ}$=3.
点评 此题考查了同角三角函数间基本关系的运用,以及完全平方公式的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
10.已知“p:函数f(x)=$\frac{x}{\sqrt{(1-a){x}^{2}-(1-a)x+1}}$的定义城为R;:“q:函数f(x)=1n|2x-a|在($\frac{1}{2}$,+∞)内为增函数”,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
7.若复数z满足$\frac{z+i}{-2{i}^{3}-z}$=i,则|$\overline{z}$+1|=( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 1 |
8.下列说法正确的是( )
| A. | |r|≤1;r越大,相关程度越大;反之,相关程度越小 | |
| B. | 线性回归方程对应的直线$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$至少经过其样本数据点(x1,y1),(x2,y2),(x3,y3),(xn,yn)中的一个点 | |
| C. | 在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高 | |
| D. | 在回归分析中,相关指数R2为0.98的模型比相关指数R2为0.80的模型拟合的效果差 |
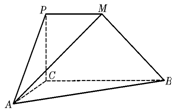 如图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=AC=1,BC=2,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.
如图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=AC=1,BC=2,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.