题目内容
(本小题满分13分)
设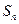 是数列
是数列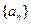 (
(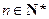 )的前
)的前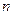 项和,
项和,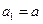 ,且
,且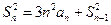 ,
,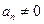 ,
,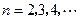 .
.
(I)证明:数列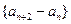 (
(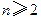 )是常数数列;
)是常数数列;
(II)试找出一个奇数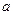 ,使以18为首项,7为公比的等比数列
,使以18为首项,7为公比的等比数列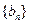 (
(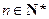 )中的所有项都是数列
)中的所有项都是数列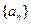 中的项,并指出
中的项,并指出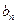 是数列
是数列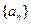 中的第几项.
中的第几项.
设
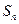 是数列
是数列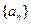 (
(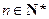 )的前
)的前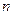 项和,
项和,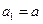 ,且
,且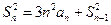 ,
,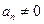 ,
,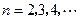 .
.(I)证明:数列
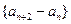 (
(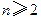 )是常数数列;
)是常数数列;(II)试找出一个奇数
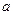 ,使以18为首项,7为公比的等比数列
,使以18为首项,7为公比的等比数列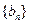 (
(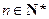 )中的所有项都是数列
)中的所有项都是数列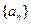 中的项,并指出
中的项,并指出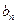 是数列
是数列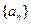 中的第几项.
中的第几项.(I)数列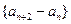 (
(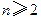 )是常数数列
)是常数数列
(II)若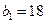 是数列
是数列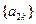 中的第
中的第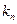 项,由
项,由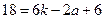 得
得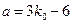 ,取
,取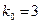 ,得
,得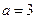 ,
,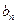 是数列
是数列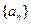 中的第
中的第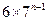 项.
项.
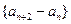 (
(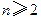 )是常数数列
)是常数数列(II)若
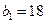 是数列
是数列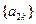 中的第
中的第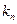 项,由
项,由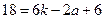 得
得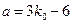 ,取
,取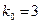 ,得
,得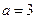 ,
,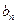 是数列
是数列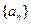 中的第
中的第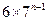 项.
项.解:(I)当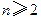 时,由已知得
时,由已知得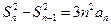 .
.
因为 ,所以
,所以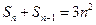 . …………………………①
. …………………………①
于是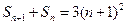 . …………………………………………………②
. …………………………………………………②
由②-①得: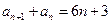 .……………………………………………③
.……………………………………………③
于是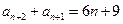 .……………………………………………………④
.……………………………………………………④
由④-③得: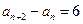 .…………………………………………………⑤
.…………………………………………………⑤
即数列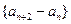 (
(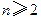 )是常数数列.
)是常数数列.
(II)由①有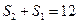 ,所以
,所以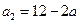 .
.
由③有 ,所以
,所以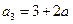 ,
,
而⑤表明:数列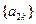 和
和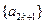 分别是以
分别是以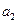 ,
,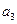 为首项,6为公差的等差数列.
为首项,6为公差的等差数列.
所以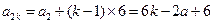 ,
, ,
, .
.
由题设知,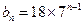 .当
.当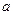 为奇数时,
为奇数时,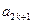 为奇数,而
为奇数,而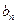 为偶数,所以
为偶数,所以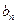 不是数列
不是数列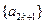 中的项,
中的项,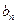 只可能是数列
只可能是数列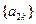 中的项.
中的项.
若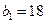 是数列
是数列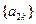 中的第
中的第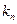 项,由
项,由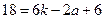 得
得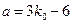 ,取
,取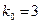 ,得
,得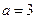 ,此时
,此时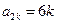 ,由
,由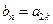 ,得
,得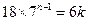 ,
,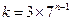
 ,从而
,从而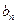 是数列
是数列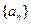 中的第
中的第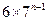 项.
项.
(注:考生取满足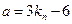 ,
,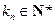 的任一奇数,说明
的任一奇数,说明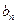 是数列
是数列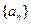 中的第
中的第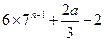 项即可)
项即可)
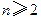 时,由已知得
时,由已知得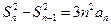 .
.因为
 ,所以
,所以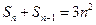 . …………………………①
. …………………………①于是
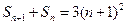 . …………………………………………………②
. …………………………………………………②由②-①得:
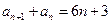 .……………………………………………③
.……………………………………………③于是
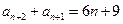 .……………………………………………………④
.……………………………………………………④由④-③得:
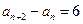 .…………………………………………………⑤
.…………………………………………………⑤即数列
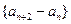 (
(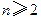 )是常数数列.
)是常数数列.(II)由①有
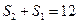 ,所以
,所以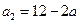 .
.由③有
 ,所以
,所以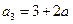 ,
,而⑤表明:数列
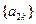 和
和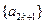 分别是以
分别是以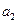 ,
,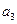 为首项,6为公差的等差数列.
为首项,6为公差的等差数列.所以
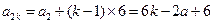 ,
, ,
, .
.由题设知,
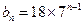 .当
.当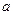 为奇数时,
为奇数时,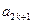 为奇数,而
为奇数,而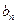 为偶数,所以
为偶数,所以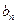 不是数列
不是数列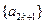 中的项,
中的项,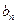 只可能是数列
只可能是数列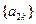 中的项.
中的项.若
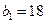 是数列
是数列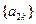 中的第
中的第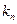 项,由
项,由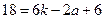 得
得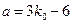 ,取
,取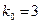 ,得
,得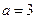 ,此时
,此时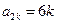 ,由
,由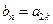 ,得
,得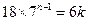 ,
,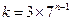
 ,从而
,从而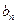 是数列
是数列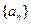 中的第
中的第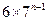 项.
项.(注:考生取满足
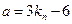 ,
,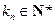 的任一奇数,说明
的任一奇数,说明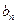 是数列
是数列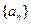 中的第
中的第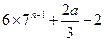 项即可)
项即可)
练习册系列答案
相关题目
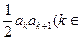 N*),其中a1=1.
N*),其中a1=1.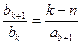 (k=1,2,…,n-1),b1=1.
(k=1,2,…,n-1),b1=1.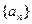 构成:
构成: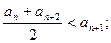
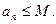 (n为正整数)
(n为正整数)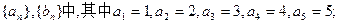
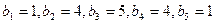 ;试判断数列
;试判断数列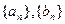 是否为集合W的元素;
是否为集合W的元素;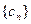 是等差数列,
是等差数列,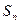 是其前n项和,
是其前n项和,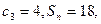 证明数列
证明数列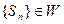 ;并写出M的取值范围;
;并写出M的取值范围;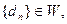 且对满足条件的常数M,存在正整数k,使
且对满足条件的常数M,存在正整数k,使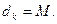
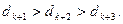
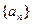 满足
满足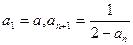 (n≥1)(
(n≥1)(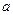 ≠2)
≠2)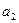 ,
,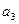 ,
,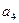 ;
; 中,
中, ,且
,且 ,
, .
.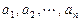 满足
满足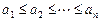 ,则
,则 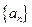 的前
的前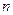 项和为
项和为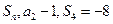 .
.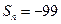 ,求
,求
 的前n项和为
的前n项和为 ,且
,且 =6,
=6, =4, 则公差等于
=4, 则公差等于 ( )
( ) C. 2 D 3
C. 2 D 3