题目内容
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() ,
,![]() 的中点.
的中点.
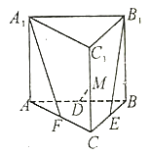
(1)证明:直线![]() 与
与![]() 共面;并求其所成角的余弦值;
共面;并求其所成角的余弦值;
(2)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,求
,若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)证明见解析,![]() ;(2)存在,
;(2)存在,![]() ,理由见解析.
,理由见解析.
【解析】
(1)证明直线![]() 与
与![]() 共面只需证明出
共面只需证明出![]() 与
与![]() 平行即可,然后再通过余弦定理求出两直线所成角的余弦值;
平行即可,然后再通过余弦定理求出两直线所成角的余弦值;
(2)建立直角坐标系,求出![]() ,利用线面垂直条件证明
,利用线面垂直条件证明![]() 即可.
即可.
(1)证明:![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,
![]() ,
,
由棱柱性质易得![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() 四点共面,
四点共面,
即直线![]() 与
与![]() 共面得证,
共面得证,
取![]() 中点为
中点为![]() ,连结
,连结![]() ,易知四边形
,易知四边形![]() 为平行四边形,
为平行四边形,
故![]() ,则
,则![]() 为直线
为直线![]() 与
与![]() 所成角,
所成角,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
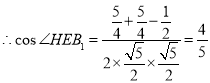 ,
,
即直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() ;
;
(2)由题意,直线![]() ,
,![]() ,
,![]() 两两相互垂直,
两两相互垂直,
如图所示建立直角坐标系,![]() 为坐标原点,
为坐标原点,
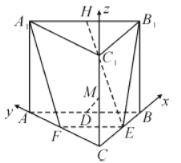
有![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
设![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
![]() ,
,
要使![]() 平面
平面![]() ,则
,则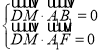 ,
,
即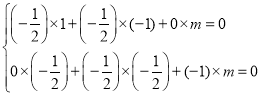 ,
,
解得![]() ,即
,即![]() ,
,
故在棱![]() 上存在点
上存在点![]() ,
,
使得![]() 平面
平面![]() ,且
,且![]() .
.

练习册系列答案
相关题目
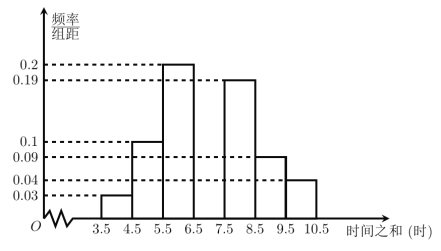
【题目】2017年3月18日,国务院办公厅发布了《生活垃圾分类制度实施方案》,我市环保部门组织了一次垃圾分类知识的网络问卷调查,每位市民都可以通过电脑网络或手机微信平台参与,但仅有一次参加机会工作人员通过随机抽样,得到参与网络问卷调查的100人的得分(满分按100分计)数据,统计结果如下表.
组别 |
|
|
|
|
|
|
女 | 2 | 4 | 4 | 15 | 21 | 9 |
男 | 1 | 4 | 10 | 10 | 12 | 8 |
(1)环保部门规定:问卷得分不低于70分的市民被称为“环保关注者”.请列出![]() 列联表,并判断能否在犯错误的概率不超过
列联表,并判断能否在犯错误的概率不超过![]() 的前提下,认为是否为“环保关注者”与性别有关?
的前提下,认为是否为“环保关注者”与性别有关?
(2)若问卷得分不低于80分的人称为“环保达人”.现在从本次调查的“环保达人”中利用分层抽样的方法随机抽取5名市民参与环保知识问答,再从这5名市民中抽取2人参与座谈会,求抽取的2名市民中,既有男“环保达人”又有女“环保达人”的概率.
附表及公式: ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|