题目内容
18.(1)在等差数列{an}中,已知d=2,n=15,an=-10,求a1及sn.(2)在等比数列{an}中,a1=2,a4=-54,求an及其前n项和Sn.
分析 (1)由题意和等差数列的通项公式可得a1,进而由求和公式可得S15;
(2)由题意和等比数列的通项公式可得公比q,可得an和Sn.
解答 解:(1)由题意可得a15=a1+14×2=-10,解得a1=-38,
∴S15=15×(-38)+$\frac{15×14}{2}$×2=-360;
(2)设等比数列{an}的公比为q,
则q3=$\frac{{a}_{4}}{{a}_{1}}$=-27,∴q=-3,
∴an=2×(-3)n-1,
Sn=$\frac{2×[1-(-3)^{n}]}{1-(-3)}$=$\frac{1}{2}$[1-(-3)n]
点评 本题考查等差数列和等比数列的通项公式和求和公式,属基础题.

练习册系列答案
相关题目
8.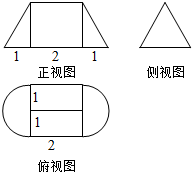 一个几何体的侧视图是边长为2的正三角形,正视图与俯视图的尺寸如图所示,则此几何体的表面积为( )
一个几何体的侧视图是边长为2的正三角形,正视图与俯视图的尺寸如图所示,则此几何体的表面积为( )
 一个几何体的侧视图是边长为2的正三角形,正视图与俯视图的尺寸如图所示,则此几何体的表面积为( )
一个几何体的侧视图是边长为2的正三角形,正视图与俯视图的尺寸如图所示,则此几何体的表面积为( )| A. | 12+2$\sqrt{3}$+3π | B. | 12+3π | C. | 2$\sqrt{3}$+$\frac{{\sqrt{3}π}}{3}$ | D. | 2$\sqrt{3}$+$\sqrt{3}$π |
10.函数y=2sinx-1的最小值为( )
| A. | -3 | B. | -2 | C. | -1 | D. | 0 |