��Ŀ����
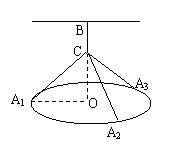
(��С������16��)��ͼ��ʾ��һ���Ƶ���Բ��ֱ��Ϊ4m��Բ��ΪO��ͨ��ϸ���������컨���ϣ�Բ����ˮƽ״̬���������컨��ľ���![]() Ϊ2m����Բ�������������ȷֵ�A1��A2��A3.��CΪ
Ϊ2m����Բ�������������ȷֵ�A1��A2��A3.��CΪ![]() ��һ�㣨�������˵�O��B����ͬʱ��C���A1��A2��A3��B����ϸ�������ӣ���ϸ��CA1��CA2��CA3�ij������.��ϸ�����ܳ�Ϊym.
��һ�㣨�������˵�O��B����ͬʱ��C���A1��A2��A3��B����ϸ�������ӣ���ϸ��CA1��CA2��CA3�ij������.��ϸ�����ܳ�Ϊym.
��1�������CA1O = ![]() (rad)����y��ʾ�ɦȵĺ�����ϵʽ��
(rad)����y��ʾ�ɦȵĺ�����ϵʽ��
����CO=x m, ��y��ʾ��x�ĺ�����ϵʽ;
 ��2������ѡ�ã�1���е�һ��������ϵȷ��BC�ij�ʹϸ���ܳ�y ��С.
��2������ѡ�ã�1���е�һ��������ϵȷ��BC�ij�ʹϸ���ܳ�y ��С.
(1) ����![]() ��COA1��
��COA1��
![]() ��
��![]() �� ������2��
�� ������2��

![]() =
=
![]() ��
��![]() �� ������4��
�� ������4��
����![]() ��COA1��CA1=
��COA1��CA1= ![]() ,BC=2-x ������6��
,BC=2-x ������6��
y=3 CA1+CB=3![]() -x+2 (0<x<2) ������8��
-x+2 (0<x<2) ������8��
��2����![]() �� ������10��
�� ������10��
��![]() ����
����![]() ������12��
������12��
��![]() ʱ��
ʱ��![]() ��
��![]() ʱ��
ʱ��![]() ��
��
��![]() ��
��![]() ����������
����������
�൱��![]() ����
����![]() ʱ��y��С����СΪ
ʱ��y��С����СΪ![]() �� ������15��
�� ������15��
��ʱBC![]() m. ������16��
m. ������16��
�� ![]() ������10��
������10��
�� ![]() ,��x=
,��x=![]() ������12��
������12��
��x>![]() ʱ,
ʱ, ![]() ;��x<
;��x<![]() ʱ,
ʱ, ![]() ;
;
��x=![]() ʱ, y��С����СΪ
ʱ, y��С����СΪ![]() �� ������15��
�� ������15��
��ʱBC![]() m. ������16��
m. ������16��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д� ��ƽ��ֱ������ϵ
��ƽ��ֱ������ϵ ��
�� (
( )��
)��
 ��������
�������� ʱ��
ʱ�� ���������ʵ��
���������ʵ�� �ķ�Χ��
�ķ�Χ�� ������
������ ��
�� �����ֵ��
�����ֵ�� ������
������ ��ʵ������
����
��ʵ������
���� ������
������ ��ֵ����
��ֵ���� ���������
��������� Ϊ�����⣬
Ϊ�����⣬ Ϊ�����⣬��ʵ��
Ϊ�����⣬��ʵ�� ��ȡֵ��Χ��
��ȡֵ��Χ�� Ϊż�������Һ���y��f(x)ͼ��������ڶԳ����ľ���Ϊ
Ϊż�������Һ���y��f(x)ͼ��������ڶԳ����ľ���Ϊ
 ����ֵ��
����ֵ�� ����λ���ٽ��õ���ͼ���ϸ���ĺ������ӳ���ԭ����4���������겻�䣬�õ�����y��g(x)��ͼ����g(x)�ĵ����ݼ�����.
����λ���ٽ��õ���ͼ���ϸ���ĺ������ӳ���ԭ����4���������겻�䣬�õ�����y��g(x)��ͼ����g(x)�ĵ����ݼ�����.