题目内容
证明一次函数f(x)=kx+b(k≠0)是奇函数的充要条件是b=0.
思路分析：要分清充分性是证明怎样的一个式子成立，必要性又是证明怎样的一个式子成立，本题的必要性：由b=0
一次函数f(x)=kx+b(k≠0)是奇函数，而充分性：由一次函数f(x)=kx+b(k≠0)是奇函数
b=0.
证明:(1)必要性:∵f(x)=kx+b(k≠0)是奇函数,
∴f(-x)=-f(x),即k(-x)+b=-(kx+b).∴b=0.
(2)充分性:如果b=0,那么f(x)=kx,此时f(x)为奇函数.
∴一次函数f(x)=kx+b(k≠0)是奇函数的充要条件是b=0
练习册系列答案
相关题目
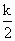＋f(x)成立．