题目内容
已知命题p:?x∈[1,2],x2-a≥0;命题q:?x∈R,使得x2+(a-1)x+1<0.若“p或q”为真,“p且q”为假,求实数a的取值范围.
【答案】分析:先求出命题p,q为真命题时,a的范围,据复合函数的真假得到p,q中必有一个为真,另一个为假,分两类求出a的范围.
解答:解:p真,则a≤1 …(2分)
q真,则△=(a-1)2-4>0
即a>3或a<-1 …(4分)
∵“p或q”为真,“p且q”为假,
∴p,q中必有一个为真,另一个为假 …(6分)
当p真q假时,有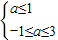 得-1≤a≤1 …(8分)
得-1≤a≤1 …(8分)
当p假q真时,有
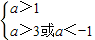 得a>3 …(10分)
得a>3 …(10分)
∴实数a的取值范围为-1≤a≤1或a>3 …(12分)
点评:本题考查复合函数的真假与构成其简单命题的真假的关系,解决此类问题应该先求出简单命题为真时参数的范围,属于基础题.
解答:解:p真,则a≤1 …(2分)
q真,则△=(a-1)2-4>0
即a>3或a<-1 …(4分)
∵“p或q”为真,“p且q”为假,
∴p,q中必有一个为真,另一个为假 …(6分)
当p真q假时,有
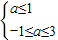 得-1≤a≤1 …(8分)
得-1≤a≤1 …(8分)当p假q真时,有
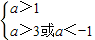 得a>3 …(10分)
得a>3 …(10分)∴实数a的取值范围为-1≤a≤1或a>3 …(12分)
点评:本题考查复合函数的真假与构成其简单命题的真假的关系,解决此类问题应该先求出简单命题为真时参数的范围,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知命题p:?x∈R,2x2+2x+
<0;命题q:?x∈R,sinx-cosx=
.则下列判断正确的是( )
| 1 |
| 2 |
| 2 |
| A、p是真命题 |
| B、q是假命题 |
| C、¬P是假命题 |
| D、¬q是假命题 |