题目内容
(本小题满分14分)
已知等差数列{an}中,a1=-1,前12项和S12=186.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足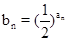 ,记数列{bn}的前n项和为Tn,
,记数列{bn}的前n项和为Tn,
求证: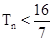 (n∈N*).
(n∈N*).
已知等差数列{an}中,a1=-1,前12项和S12=186.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足
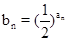 ,记数列{bn}的前n项和为Tn,
,记数列{bn}的前n项和为Tn,求证:
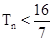 (n∈N*).
(n∈N*). (Ⅰ) an=-1+(n-1)×3=3n-4. (Ⅱ)见解析。
第一问考查数列中基本量的运算,这类问题主要是要把数列的通项与前n项和都用其首项与公差(或公比)表示出来;第二问先判断数列{bn}是等比数列,求出其前n项和,然后就很容易证明。
解:(Ⅰ)设等差数列{an}的公差为d,∵ a1=-1,S12=186,
∴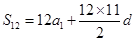 , ……2分
, ……2分
即 186=-12+66d. ……4分∴d=3. ……5分
所以数列{an}的通项公式 an=-1+(n-1)×3=3n-4. ……7分
(Ⅱ)∵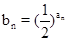 ,an=3n-4,∴
,an=3n-4,∴ . ……8分
. ……8分
∵ 当n≥2时, , ……9分
, ……9分
∴ 数列{bn}是等比数列,首项 ,公比
,公比 . ……10分
. ……10分
∴ . ……12分
. ……12分
∵ ,∴
,∴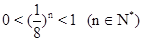 ,
,
∴ . ……13分
. ……13分
所以 . ……14分
. ……14分
解:(Ⅰ)设等差数列{an}的公差为d,∵ a1=-1,S12=186,
∴
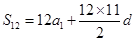 , ……2分
, ……2分即 186=-12+66d. ……4分∴d=3. ……5分
所以数列{an}的通项公式 an=-1+(n-1)×3=3n-4. ……7分
(Ⅱ)∵
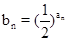 ,an=3n-4,∴
,an=3n-4,∴ . ……8分
. ……8分∵ 当n≥2时,
 , ……9分
, ……9分∴ 数列{bn}是等比数列,首项
 ,公比
,公比 . ……10分
. ……10分∴
 . ……12分
. ……12分∵
 ,∴
,∴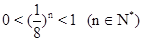 ,
,∴
 . ……13分
. ……13分所以
 . ……14分
. ……14分
练习册系列答案
相关题目
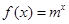 (m为常数,m>0且m≠1).
(m为常数,m>0且m≠1).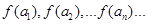 (n∈
(n∈ ?)是首项为m2,公比为m的等比数列.
?)是首项为m2,公比为m的等比数列.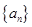 是等差数列;
是等差数列; 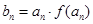 ,且数列
,且数列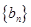 的前n项和为Sn,当m=2时,求Sn;
的前n项和为Sn,当m=2时,求Sn;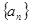 的前
的前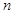 项和
项和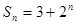 ,则数列
,则数列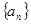 的前n项的和Sn = 2n2-n+1,则an=
的前n项的和Sn = 2n2-n+1,则an= 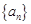 的前
的前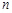 项和为
项和为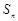 ,则
,则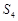 ,
,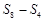 ,
,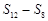 ,
,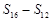 成等差数列.类比以上结论有:设等比数列
成等差数列.类比以上结论有:设等比数列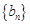 的前
的前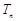 ,则
,则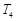 , , ,
, , ,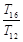 成等比数列.
成等比数列.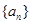 的前
的前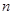 项和为
项和为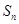 ,且有
,且有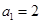 ,
,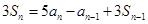
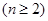
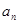 的通项公式;
的通项公式;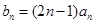 ,求数列
,求数列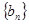 的前
的前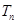 。山大附中
。山大附中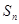 是等差数列
是等差数列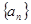 的前
的前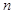 项和,
项和,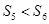 ,
,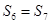 ,
,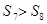 则下列结论中错误的( )
则下列结论中错误的( )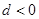
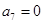
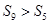
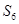 与
与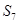 均为
均为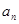 }是等差数列,
}是等差数列,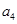 =7,则
=7,则 =_________
=_________