题目内容

函数f（x）（x∈R）的图象如图所示，则函数g（x）=f（loga x）（0＜a＜1）的单调减区间是(    )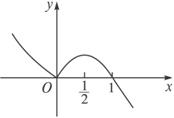

A.［0，］                           B.（-∞，0）∪［，+∞）

C.［，1］                          D.［，］

思路解析：由图象可知在（-∞，0）和（，+∞）上f（x）均是减函数，在［0，］上f（x）是增函数.

又∵0＜a＜1，∴loga x是减函数.利用复合函数的单调性可知满足不等式0≤loga x≤的x的值即为单调减区间，即减区间为［a，1］.

答案：C

练习册系列答案
相关题目
已知x＞
12
，函数f（x）=x2，h（x）=2e lnx（e为自然常数）．
（Ⅰ）求证：f（x）≥h（x）；
（Ⅱ）若f（x）≥h（x）且g（x）≤h（x）恒成立，则称函数h（x）的图象为函数f（x），g（x）的“边界”．已知函数g（x）=-4x2+px+q（p，q∈R），试判断“函数f（x），g（x）以函数h（x）的图象为边界”和“函数f（x），g（x）的图象有且仅有一个公共点”这两个条件能否同时成立？若能同时成立，请求出实数p、q的值；若不能同时成立，请说明理由．
设函数f（x）=x|x|+bx+c（b，c∈R），则下列命题中正确的是（　　）
A、“b≥0”是“函数y=f（x）在R上单调递增”的必要非充分条件
B、“b＜0，c＜0”是“方程f（x）=0有两个负根”的充分非必要条件
C、“c=0”是“函数y=f（x）为奇函数”的充要条件
D、“c＞0”是“不等式f(x)≥( 2
c
+b)x对任意x∈R+恒成立”的既不充分也不必要条件
定义在R上的奇函数f（x）满足f（2-x）=f（x），当x∈[0，1]时，f(x)=
x
．又g(x)=cos
πx
2
，则集合{x|f（x）=g（x）}等于（　　）
如果函数f（x）在x=x0处取得极值，则点（x0，f（x0））称为函数f（x）的一个极值点．已知函数f（x）=ax3+bx2+cx+d（a≠0，a，b，c，d∈R）的一个极值点恰为坐标系原点，且y=f（x）在x=1处的切线方程为3x+y-1=0．
（1）求函数f（x）的解析式；
（2）求函数f（x）在[-2，2]上的值域．
下列命题中，错误命题的序号有
 
．
（1）“a=-1”是“函数f（x）=x2+|x+a+1|（ x∈R） 为偶函数”的必要条件；
（2）“直线l垂直平面α内无数条直线”是“直线l垂直平面α”的充分条件；
（3）已知a，b，c为非零向量，则“a•b=a•c”是“b=c”的充要条件；
（4）若p：?x∈R，x2+2x+2≤0，则￢p：?x∈R，x2+2x+2＞0．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网