题目内容
17．我们把平面区域中横纵坐标均为整数的点称为整点，那么在不等式组$\left\{\begin{array}{l}2x-y+2＞0\\ x+y-2≤0\\ y≥0\end{array}\right.$表示的平面区域中，整点的个数为（ ）| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
分析 作出不等式组对应的平面区域，利用分类讨论的方法，即可得到结论．
解答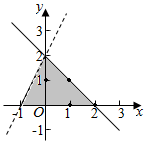 
解：当y=0时，不等式组为$\left\{\begin{array}{l}{x＞-1}\\{x≤2}\end{array}\right.$，即-1＜x≤2，此时x=0或x=1或x=2．
当y=1时，不等式组为$\left\{\begin{array}{l}{x＞-\frac{1}{2}}\\{x≤1}\end{array}\right.$，即$-\frac{1}{2}$＜x≤1，此时x=0或x=1．
当y=2时，不等式组为$\left\{\begin{array}{l}{x＞0}\\{x≤0}\end{array}\right.$，此时无解．
综上整数点的个数为5个，
故选：B．
点评 本题主要考查二次一元不等式组表示平面区域，利用分类讨论的数学进行求解是解决本题的关键．比较基础．
练习册系列答案
口算能手系列答案
相关题目
8．已知点F为双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点，过F作直线l与双曲线C相交于A，B两点，若满足|AB|=2的直线l有且仅有两条，则双曲线C的方程可以是（ ）
| A． | x2-4y2=1 | B． | x2-$\frac{{y}^{2}}{2}$=1 | C． | 2x2-2y2=1 | D． | x2-y2=1 |
12．已知数列1，0，1，0，…，下列选项中，不能作为它的通项的是（ ）
| A． | $\frac{1}{2}[{1+{{（-1）}^{n+1}}}]$ | B． | ${sin^2}\frac{nπ}{2}$ | C． | $\frac{1}{2}[{1+{{（-1）}^n}}]$ | D． | $\frac{1-cosnπ}{2}$ |
9．命题“?x2＞1，x≤1”的否定是（ ）
| A． | ?x2＞1，x≤1 | B． | ?x2≤1，x≤1 | C． | ?x2＞1，x＞1 | D． | ?x2≤1，x≤1 |
6．函数$f（x）=sinx-cos（x+\frac{π}{6}）$的最小值为（ ）
| A． | -2 | B． | $\sqrt{3}$ | C． | 1 | D． | $-\sqrt{3}$ |