题目内容
(本小题满分12分) 已知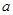 为实数,
为实数,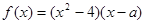 ,
,
(Ⅰ)若a=2,求 的单调递增区间;
的单调递增区间;
(Ⅱ)若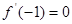 ,求
,求 在[-2,2] 上的最大值和最小值。
在[-2,2] 上的最大值和最小值。
(Ⅰ) ,
, (Ⅱ)最大值为
(Ⅱ)最大值为 最小值为
最小值为
解析试题分析:(Ⅰ)由 ,得
,得 或
或
所以当a=2时f(x)的单调递增区间为 或
或 (6分)
(6分)
(Ⅱ)由原式得 ∴
∴
由 得
得 ,此时有
,此时有 .
.
令 得
得 或x="-1" , 又
或x="-1" , 又
所以f(x)在[-2,2]上的最大值为 最小值为
最小值为 (12分)
(12分)
考点:函数的单调性和最值
点评:利用函数的导数可以求单调区间,极值,最值等问题

练习册系列答案
相关题目
 .
. ,求
,求 的最小值;
的最小值; ,讨论函数
,讨论函数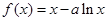 ,
,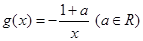 .
.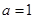 ,求函数
,求函数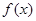 的极值;
的极值;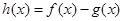 ,求函数
,求函数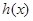 的单调区间;
的单调区间;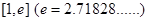 上不存在
上不存在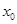 ,使得
,使得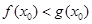 成立,求实数
成立,求实数 的取值范围.
的取值范围.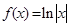
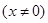 ,函数
,函数
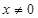 时,求函数
时,求函数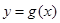 的表达式;
的表达式;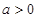 ,且函数
,且函数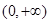 上的最小值是2 ,求
上的最小值是2 ,求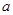 的值;
的值;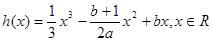 ,恰有三个零点,求b的取值范围。
,恰有三个零点,求b的取值范围。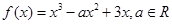
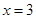 是
是 的极值点,求
的极值点,求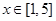 上的最大值
上的最大值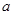 的取值范围.
的取值范围.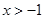 ,证明:
,证明: 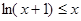
 是实数,函数
是实数,函数 。
。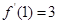 ,求
,求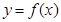 在点
在点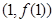 处的切线方程;
处的切线方程; 在区间
在区间 上的最大值。
上的最大值。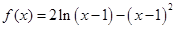 .
.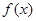 的单调递增区间;
的单调递增区间;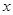 的方程
的方程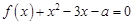 在区间
在区间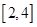 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数 的取值范围.
的取值范围.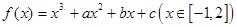 ,且函数
,且函数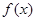 在
在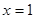 和
和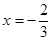 处都取得极值。
处都取得极值。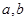 的值;
的值;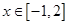 ,
,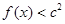 恒成立,求实数
恒成立,求实数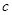 的取值范围。
的取值范围。