题目内容
已知向量
=（cosθ，sinθ），
=（cos2θ，sin2θ），
=（-1，0），
=（0，1）．
（1）求证：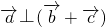
； （2）设f（θ）=
，求f（θ）的值域．
解：（1）∵
…（2分）
又∵
…（4分）
∴
，
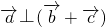∴…（6分）
（2）f（θ）=
）…（10分）
所以f（θ）的值域为[-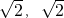
]…（14分）
分析：（1）利用向量的分配律及向量的数量积公式求出
；利用向量的数量积为0向量垂直得证．
（2）利用向量的数量积公式将已知等式得到
，利用三角函数的性质求出f（θ）的值域．
点评：本题考查向量垂直的充要条件、向量模的平方等于向量的平方、向量的数量积公式．
…（2分）又∵
…（4分）∴
，∴
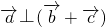…（6分）（2）f（θ）=
）…（10分）所以f（θ）的值域为[-
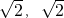]…（14分）分析：（1）利用向量的分配律及向量的数量积公式求出
；利用向量的数量积为0向量垂直得证．（2）利用向量的数量积公式将已知等式得到
，利用三角函数的性质求出f（θ）的值域．点评：本题考查向量垂直的充要条件、向量模的平方等于向量的平方、向量的数量积公式．
练习册系列答案
相关题目
已知向量
=（cosα，sinα），
=（cosβ，sinβ），若|
-
|=
，则
和
的夹角为（ ）
| a |
| b |
| a |
| b |
| 2 |
| a |
| b |
| A、60° | B、90° |
| C、120° | D、150° |