题目内容
(选修4—4 参数方程与极坐标)(本题满分7分)
在极坐标系下,已知圆O: 和直线
和直线 ,
,
(Ⅰ)求圆O和直线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)当 时,求直线
时,求直线 与圆O公共点的一个极坐标.
与圆O公共点的一个极坐标.
【答案】
(Ⅰ) ;
;
(Ⅱ)
【解析】本试题主要是考查了极坐标与直角坐标系的互化,以及直线与圆的位置关系的运用。
(1)因为圆O的极坐标方程已知,两边同时乘以极径,可以化为直角坐标关系式,也就可以得到结论
(2)根据第一问的直角坐标方程与直线方程联立方程组,求解交点的坐标得到结论。
解:(Ⅰ)圆O: ,即
,即
圆O的直角坐标方程为: ,即
,即 …………2分
…………2分
直线 ,即
,即
则直线 的直角坐标方程为:
的直角坐标方程为: ,即
,即 …………4分
…………4分
(Ⅱ)由 得
得 …………6分
…………6分
故直线 与圆O公共点的一个极坐标为
与圆O公共点的一个极坐标为 …………7分
…………7分

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
从A,B,C,D四个中选做2个,每题10分,共20分
| A.选修4—1 几何证明选讲 如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D。求证:  。 。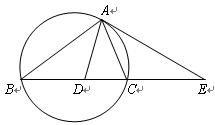 |
| B.选修4—2 矩阵与变换 在平面直角坐标系 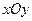 中,设椭圆 中,设椭圆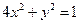 在矩阵对应的变换作用下得到曲线F,求F的方程。 在矩阵对应的变换作用下得到曲线F,求F的方程。 |
| C.选修4—4 参数方程与极坐标 在平面直角坐标系 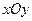 中,点 中,点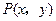 是椭圆 是椭圆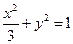 上的一个动点,求 上的一个动点,求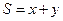 的最大值。 的最大值。 |
| D.选修4—5 不等式证明选讲 |
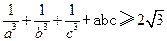 。
。