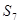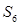题目内容
已知各项都不为零的数列 的前n项和为
的前n项和为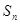 ,
,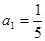 ,向量
,向量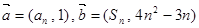 ,其中
,其中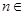 N*,且
N*,且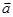 ∥
∥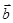 .
.
(Ⅰ)求数列 的通项公式及
的通项公式及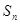 ;
;
(Ⅱ)若数列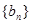 的前n项和为
的前n项和为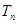 ,且
,且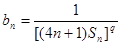 (其中
(其中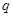 是首项
是首项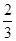 ,第四项为
,第四项为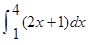 的等比数列的公比),求证:
的等比数列的公比),求证: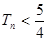 .
.
 的前n项和为
的前n项和为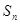 ,
,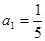 ,向量
,向量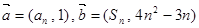 ,其中
,其中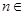 N*,且
N*,且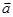 ∥
∥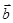 .
.(Ⅰ)求数列
 的通项公式及
的通项公式及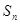 ;
; (Ⅱ)若数列
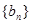 的前n项和为
的前n项和为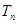 ,且
,且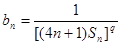 (其中
(其中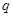 是首项
是首项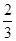 ,第四项为
,第四项为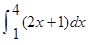 的等比数列的公比),求证:
的等比数列的公比),求证: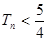 .
.当 时,
时, (1)
(1)  (2)见解析
(2)见解析
 时,
时, (1)
(1)  (2)见解析
(2)见解析本试题主要考查了数列的通项公式和前n项和公式的运用。
(1)因为 ,对n="1,"
,对n="1,"  分别求解通项公式,然后合并。利用
分别求解通项公式,然后合并。利用 ,求解
,求解
(2)利用

裂项后求和得到结论。
解:(1) ……1分
……1分
当 时,
时, ……2分
……2分
 (
( )……5分
)……5分
 ……7分
……7分
 ……9分
……9分
证明:当 时,
时, 
(1)因为
 ,对n="1,"
,对n="1,"  分别求解通项公式,然后合并。利用
分别求解通项公式,然后合并。利用 ,求解
,求解
(2)利用

裂项后求和得到结论。
解:(1)
 ……1分
……1分当
 时,
时, ……2分
……2分 (
( )……5分
)……5分 ……7分
……7分 ……9分
……9分证明:当
 时,
时, 

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
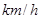 ,这个车队当天一共行驶了多少千米?
,这个车队当天一共行驶了多少千米?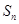 是正项数列
是正项数列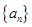 的前
的前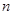 项和,且
项和,且 (
(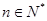 ).
).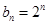 ,设
,设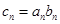 ,求数列
,求数列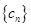 的前
的前 .
.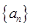 的前n项和
的前n项和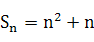 ,在各项为正数的数列
,在各项为正数的数列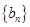 中
中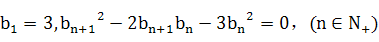
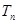
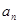 )满足
)满足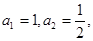 并且
并且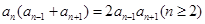 ,则数列的第2012项为
,则数列的第2012项为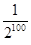
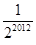
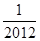
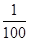
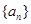 的公差
的公差 ,若
,若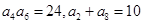 ,则该数列的前
,则该数列的前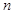 项和
项和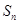 的最大值为( )
的最大值为( )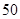
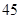
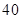
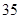
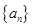 中,若
中,若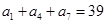 ,,
,, 则前9项和等于( )
则前9项和等于( ) 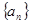 的前
的前 项之和为
项之和为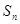 ,已知
,已知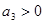 ,
,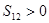 ,
,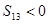 ,则
,则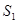 ,
,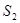 ,
, ,
,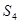 ,…,
,…,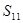 ,
,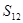 中最大的是 ( )
中最大的是 ( )