题目内容
已知椭圆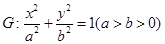 的离心率为
的离心率为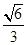 ,右焦点为
,右焦点为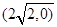 。斜率为1的直线
。斜率为1的直线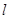 与椭圆
与椭圆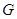 交于
交于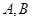 两点,以
两点,以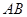 为底边作等腰三角形,顶点为
为底边作等腰三角形,顶点为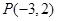 。
。
(1)求椭圆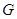 的方程;
的方程;
(2)求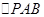 的面积。
的面积。
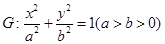 的离心率为
的离心率为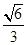 ,右焦点为
,右焦点为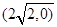 。斜率为1的直线
。斜率为1的直线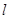 与椭圆
与椭圆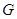 交于
交于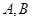 两点,以
两点,以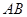 为底边作等腰三角形,顶点为
为底边作等腰三角形,顶点为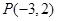 。
。(1)求椭圆
 的方程;
的方程;(2)求
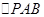 的面积。
的面积。(1) (2)
(2)
 (2)
(2)
(1)由已知得 解得
解得 又
又
所以椭圆G的方程为
(2)设直线l的方程为 由
由 得
得 设A、B的坐标分别为
设A、B的坐标分别为 AB中点为E
AB中点为E ,则
,则
 因为AB是等腰△PAB的底边,所以PE⊥AB.所以PE的斜率
因为AB是等腰△PAB的底边,所以PE⊥AB.所以PE的斜率 解得m=2。此时方程①为
解得m=2。此时方程①为 解得
解得 所以
所以 所以|AB|=
所以|AB|= .此时,点P(—3,2)到直线AB:
.此时,点P(—3,2)到直线AB: 的距离
的距离 所以△PAB的面积S=
所以△PAB的面积S=
 解得
解得 又
又
所以椭圆G的方程为

(2)设直线l的方程为
 由
由 得
得 设A、B的坐标分别为
设A、B的坐标分别为 AB中点为E
AB中点为E ,则
,则
 因为AB是等腰△PAB的底边,所以PE⊥AB.所以PE的斜率
因为AB是等腰△PAB的底边,所以PE⊥AB.所以PE的斜率 解得m=2。此时方程①为
解得m=2。此时方程①为 解得
解得 所以
所以 所以|AB|=
所以|AB|= .此时,点P(—3,2)到直线AB:
.此时,点P(—3,2)到直线AB: 的距离
的距离 所以△PAB的面积S=
所以△PAB的面积S=

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
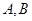 两点,左焦点在以
两点,左焦点在以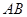 为直径的圆内,则该双曲线的离心率的取值范围为( )
为直径的圆内,则该双曲线的离心率的取值范围为( )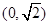
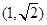
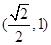
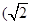 ,
,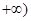
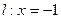 相切。
相切。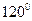 的直线与曲线M相交于A,B两点,A,B在直线
的直线与曲线M相交于A,B两点,A,B在直线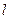 上的射影是
上的射影是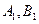 。求梯形
。求梯形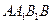 的面积;
的面积;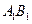 上的动点,当△ABC为直角三角形时,求点C的坐标。
上的动点,当△ABC为直角三角形时,求点C的坐标。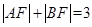 ,则线
,则线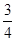
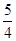
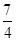
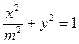 (常数
(常数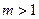 ),P是曲线C上的动点,M是曲线C的右
),P是曲线C上的动点,M是曲线C的右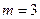 ,求|PA|的最大值与最小值.
,求|PA|的最大值与最小值.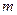 的取值范围.
的取值范围.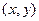 满足
满足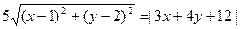 ,则M点的轨迹曲线为 .
,则M点的轨迹曲线为 .
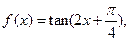 ,
,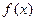 的定义域与最小正周期;
的定义域与最小正周期;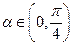 ,若
,若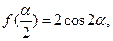 求
求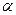 的大小.
的大小.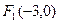 、
、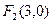 为焦点,渐近线方程为
为焦点,渐近线方程为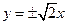 的双曲线的标准方程是 ▲ .
的双曲线的标准方程是 ▲ .