题目内容
18.已知O是锐角△ABC的外心,AB=6,AC=10.若$\overrightarrow{AO}=x\overrightarrow{AB}+y\overrightarrow{AC}$,且2x+10y=5,则cos∠BAC=( )| A. | $\frac{1}{4}$ | B. | $-\frac{1}{3}$ | C. | $-\frac{1}{4}$ | D. | $\frac{1}{3}$ |
分析 如图所示,过O点分别作OD⊥AB,OE⊥AC,垂足分别为D,E.利用垂经定理可得:AD=DB,AE=EC.于是$\overrightarrow{AO}•\overrightarrow{AB}$=$\frac{1}{2}{\overrightarrow{AB}}^{2}$=18.$\overrightarrow{AO}•\overrightarrow{AC}$=$\frac{1}{2}{\overrightarrow{AC}}^{2}$=50.由于$\overrightarrow{AO}=x\overrightarrow{AB}+y\overrightarrow{AC}$,分别作数量积可得:$\overrightarrow{AO}•\overrightarrow{AB}$=$x{\overrightarrow{AB}}^{2}$+$y\overrightarrow{AC}•\overrightarrow{AB}$,$\overrightarrow{AO}•\overrightarrow{AC}$=$x\overrightarrow{AB}•\overrightarrow{AC}+y{\overrightarrow{AC}}^{2}$,与2x+10y=5,联立解得即可.
解答 解:如图所示,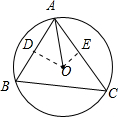
过O点分别作OD⊥AB,OE⊥AC,垂足分别为D,E.
则AD=DB,AE=EC.
$\overrightarrow{AO}•\overrightarrow{AB}$=$\frac{1}{2}{\overrightarrow{AB}}^{2}$=$\frac{1}{2}×{6}^{2}$=18.
$\overrightarrow{AO}•\overrightarrow{AC}$=$\frac{1}{2}{\overrightarrow{AC}}^{2}$=$\frac{1}{2}×1{0}^{2}$=50.
∵$\overrightarrow{AO}=x\overrightarrow{AB}+y\overrightarrow{AC}$,
∴$\overrightarrow{AO}•\overrightarrow{AB}$=$x{\overrightarrow{AB}}^{2}$+$y\overrightarrow{AC}•\overrightarrow{AB}$,$\overrightarrow{AO}•\overrightarrow{AC}$=$x\overrightarrow{AB}•\overrightarrow{AC}+y{\overrightarrow{AC}}^{2}$,
化为18=36x+60ycosA,50=60xcosA+100y,
又2x+10y=5,联立解得cosA=$\frac{1}{3}$,x=$\frac{1}{2}$,y=$\frac{9}{20}$.
故选:D.
点评 本题考查了垂经定理、数量积运算性质、方程的思想,考查了推理能力与计算能力,属于中档题.

| A. | [-$\frac{π}{2}$+2kπ,2kπ](k∈Z) | B. | [-$\frac{π}{2}$+2kπ,$\frac{π}{2}$+2kπ](k∈Z) | ||
| C. | [2kπ,$\frac{π}{2}$+2kπ](k∈Z) | D. | (-∞,+∞) |
| A. | a2<b2<-ab | B. | b2<-ab<a2 | C. | a2<-ab<b2 | D. | -ab<b2<a2 |
| A. | 10 | B. | 7 | C. | 6 | D. | 3 |