题目内容
(2013•汕头二模)某网站体育版块足球栏目组发起了“射手的上一场进连续进球有关系”的调查活动,在所有参与调查的人中,持“有关系”“无关系”“不知道”态度的人数如表所示:
(I)在所有参与调查的人中,用分层抽样的方法抽取n个人,已知从持“有关系”态度的人中抽取45人,求n的值;
(II)在持“不知道”态度的人中,用分层抽样的方法抽取5人看成一个总体,从这5人中任选取2人,求至少一人在40岁以下的概率;
(III)在接受调查的人中,有8人给这项活动打出分数如下:9.4、8.6、9.2、9.6、8,7、9.3、9.0、8.2,把这8个人打出的分数看做一个总体,从中任取1个数,求该数与总体平均数之差的绝对值超过0.6的概率.
| 有关系 | 无关系 | 不知道 | |
| 40岁以下 | 800 | 450 | 200 |
| 40岁以上(含40岁) | 100 | 150 | 300 |
(II)在持“不知道”态度的人中,用分层抽样的方法抽取5人看成一个总体,从这5人中任选取2人,求至少一人在40岁以下的概率;
(III)在接受调查的人中,有8人给这项活动打出分数如下:9.4、8.6、9.2、9.6、8,7、9.3、9.0、8.2,把这8个人打出的分数看做一个总体,从中任取1个数,求该数与总体平均数之差的绝对值超过0.6的概率.
分析:(I)根据在抽样过程中每个个体被抽到的概率相等,写出比例式,使得比例相等,得到关于n的方程,解方程即可.
(II)由题意知本题是一个等可能事件的概率,本题解题的关键是列举出所有事件的事件数,再列举出满足条件的事件数,得到概率.
(III)先求出总体的平均数,然后找到与总体平均数之差的绝对值超过0.6的数,最后根据古典概型的公式进行求解即可.
(II)由题意知本题是一个等可能事件的概率,本题解题的关键是列举出所有事件的事件数,再列举出满足条件的事件数,得到概率.
(III)先求出总体的平均数,然后找到与总体平均数之差的绝对值超过0.6的数,最后根据古典概型的公式进行求解即可.
解答:解:(Ⅰ)由题意得
=
,…(2分)
所以n=100.…(3分)
(Ⅱ)设所选取的人中,有m人20岁以下,则
=
,解得m=2.…(5分)
也就是20岁以下抽取了2人,另一部分抽取了3人,分别记作A1,A2;B1,B2,B3,
则从中任取2人的所有基本事件为 (A1,B1),(A1,B2),(A1,B3),(A2,B1),
(A2,B2),(A2,B3),(A1,A2),(B1,B2),(B2,B3),(B1,B3)共10个.…(7分)
其中至少有1人20岁以下的基本事件有7个:(A1,B1),(A1,B2),(A1,B3),
(A2,B1),(A2,B2),(A2,B3),(A1,A2),…(8分)
所以从中任意抽取2人,至少有1人20岁以下的概率为
.…(9分)
(Ⅲ)总体的平均数为
=
(9.4+8.6+9.2+9.6+8.7+9.3+9.0+8.2)=9,…(10分)
那么与总体平均数之差的绝对值超过0.6的数只有8.2,…(12分)
所以该数与总体平均数之差的绝对值超过0.6的概率为
.…(13分)
| 800+100 |
| 45 |
| 800+450+200+100+150+300 |
| n |
所以n=100.…(3分)
(Ⅱ)设所选取的人中,有m人20岁以下,则
| 200 |
| 200+300 |
| m |
| 5 |
也就是20岁以下抽取了2人,另一部分抽取了3人,分别记作A1,A2;B1,B2,B3,
则从中任取2人的所有基本事件为 (A1,B1),(A1,B2),(A1,B3),(A2,B1),
(A2,B2),(A2,B3),(A1,A2),(B1,B2),(B2,B3),(B1,B3)共10个.…(7分)
其中至少有1人20岁以下的基本事件有7个:(A1,B1),(A1,B2),(A1,B3),
(A2,B1),(A2,B2),(A2,B3),(A1,A2),…(8分)
所以从中任意抽取2人,至少有1人20岁以下的概率为
| 7 |
| 10 |
(Ⅲ)总体的平均数为
. |
| x |
| 1 |
| 8 |
那么与总体平均数之差的绝对值超过0.6的数只有8.2,…(12分)
所以该数与总体平均数之差的绝对值超过0.6的概率为
| 1 |
| 8 |
点评:本题考查分层抽样方法和等可能事件的概率,本题解题的关键是列举出事件数,要做到不重不漏,属于中档题.

练习册系列答案
相关题目
 (2013•汕头二模)执行框图,若输出结果为
(2013•汕头二模)执行框图,若输出结果为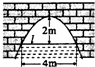 (2013•汕头二模)如图是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面宽4米,水位下降2米后水面宽
(2013•汕头二模)如图是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面宽4米,水位下降2米后水面宽