题目内容
设直线x=1是函数f(x)的图象的一条对称轴,对于任意x∈R,f(x+2)=-f(x),当-1≤x≤1时,f(x)=x3.
(1)证明:f(x)是奇函数;
(2)当x∈[3,7]时,求函数f(x)的解析式.
(1)f(x)是奇函数(2)f(x)=![]()
解析:
(1)证明 ∵x=1是f(x)的图象的一条对称轴,
∴f(x+2)=f(-x).又∵f(x+2)=-f(x),
∴f(x)=-f(x+2)=-f(-x),即f(-x)=-f(x).∴f(x)是奇函数.
(2)解 ∵f(x+2)=-f(x),∴f(x+4)=f[(x+2)+2]
=-f(x+2)=f(x),∴T=4.若x∈[3,5],则(x-4)∈[-1,1],
∴f(x-4)=(x-4.)3又∵f(x-4)=f(x),
∴f(x)=(x-4)3,x∈[3,5].若x∈(5,7],则(x-4)∈(1,3],f(x-4)=f(x).
由x=1是f(x)的图象的一条对称轴可知f[2-(x-4)]=f(x-4)
且2-(x-4)=(6-x)∈[-1,1],故f(x)=f(x-4)=f(6-x)=(6-x)3=-(x-6)3.
综上可知f(x)=![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
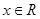 ,f(x+2)=-- f(x),当
,f(x+2)=-- f(x),当 .
. 时,求f(x)的解析式。
时,求f(x)的解析式。