题目内容
已知![]() ,函数
,函数![]() .
.
(1)若函数![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 平行,求
平行,求![]() 的值;
的值;
(2)求函数![]() 的单调递增区间;
的单调递增区间;
(3)在(1)的条件下,若对任意![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值组成的集合.
的取值组成的集合.
解:(1)![]() ,由已知
,由已知![]() ,即
,即![]() ,
,![]() ,解得
,解得![]() 或
或![]() .
.
又因为![]() ,所以
,所以![]() .
.
(2)函数![]() 的定义域为
的定义域为![]() ,
,
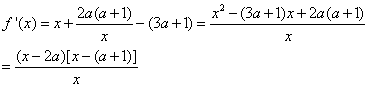 ①当
①当![]() ,即
,即![]() 时,由
时,由![]() 得
得![]() 或
或![]() ,因此函数
,因此函数![]() 的单调增区间是
的单调增区间是![]() 和
和![]() .
.
②当![]() ,即
,即![]() 时,
时,
由![]() 得
得![]() 或
或![]() ,
,
因此函数![]() 的单调增区间是
的单调增区间是![]() 和
和![]() .
.
③当![]() ,即
,即![]() 时
时![]() 恒成立(只在
恒成立(只在![]() 处等于0),所以函数在定义域
处等于0),所以函数在定义域![]() 上是增函数.
上是增函数.
综上:①当![]() 时,函数
时,函数![]() 的单调增区间是
的单调增区间是![]() 和
和![]() ;
;
②当![]() 时,函数
时,函数![]() 的单调增区间是
的单调增区间是![]() 和
和![]() ;
;
③当![]() 时,函数
时,函数![]() 的单调增区间是
的单调增区间是![]() .
.
(3)当![]() 时,
时,![]() ,由(2)知该函数在
,由(2)知该函数在![]() 上单调递增,因此在区间
上单调递增,因此在区间![]() 上
上![]() 的最小值只能在
的最小值只能在![]() 处取到. …
处取到. …
又![]() ,
,
若要保证对任意![]() ,
,![]() 恒成立,应该有
恒成立,应该有![]() ,即
,即![]() ,解得
,解得![]() ,
,
因此实数![]() 的取值组成的集合是
的取值组成的集合是![]() .
.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
已知以下函数:(1)f(x)=3lnx;(2)f(x)=3ecosx;(3)f(x)=3ex;(4)f(x)=3cosx.
其中对于f(x)定义域内的任意一个自变量x1,都存在唯一一个自变量x2使
=3成立的函数是( )
其中对于f(x)定义域内的任意一个自变量x1,都存在唯一一个自变量x2使
| f(x1)f(x2) |
| A、(1)(2)(4) |
| B、(2)(3) |
| C、(3) |
| D、(4) |
已知分段函数f(x)=
,则
f(x-2)dx等于( )
|
| ∫ | 3 1 |
A、
| ||||
| B、2-e | ||||
C、3+
| ||||
D、2-
|
已知符号函数sgn x=
则方程x+1=(2x-1)sgnx的所有解之和是( )
|
| A、0 | ||||
| B、2 | ||||
C、-
| ||||
D、
|