题目内容
已知分段函数f(x)=
,则
f(x-2)dx等于( )
|
| ∫ | 3 1 |
A、
| ||||
| B、2-e | ||||
C、3+
| ||||
D、2-
|
分析:先求出f(x-2)的解析式,然后根据分段函数分段的标准将
f(x-2)dx=∫12(x2-4x+5)dx+∫23(e2-x)dx,最后根据定积分的定义进行求解即可.
| ∫ | 3 1 |
解答:解:∵分段函数f(x)=
,
∴f(x-2)=
f(x-2)dx=∫12(x2-4x+5)dx+∫23(e2-x)dx
=(
x3-2x2+5x)
+(-e2-x)|23
=
-
故选A
|
∴f(x-2)=
|
| ∫ | 3 1 |
=(
| 1 |
| 3 |
| | | 2 1 |
=
| 7 |
| 3 |
| 1 |
| e |
故选A
点评:本题主要考查了定积分的应用,以及分段函数的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
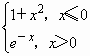 ,则
,则