题目内容
(本题满分16分,第1问4分,第2问6分,第3问6分)
已知函数![]() ,过点P(1,0)作曲线
,过点P(1,0)作曲线![]() 的两条切线PM,PN,切点分别为M,N.
的两条切线PM,PN,切点分别为M,N.
(1)当![]() 时,求函数
时,求函数![]() 的单调递增区间;
的单调递增区间;
(2)设|MN|=![]() ,试求函数
,试求函数![]() 的表达式;
的表达式;
(3)在(2)的条件下,若对任意的正整数![]() ,在区间
,在区间![]() 内,总存在m+1个数
内,总存在m+1个数![]() 使得不等式
使得不等式![]() 成立,求m的最大值.
成立,求m的最大值.
解:(1)当![]()
![]()
![]() .则函数
.则函数![]() 有单调递增区间为
有单调递增区间为![]() -
-
(2)设M、N两点的横坐标分别为![]() 、
、![]() ,
,
| |

同理,由切线PN也过点(1,0),得![]() (2)
(2)
由(1)、(2),可得![]() 的两根,
的两根,

![]()
![]()
把(*)式代入,得![]()
因此,函数![]()
(3)易知![]() 上为增函数,
上为增函数,

![]()
![]()

由于m为正整数,![]() . 又当
. 又当![]()
因此,m的最大值为6.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 的前
的前 项和为
项和为 ,且满足
,且满足 ,
, ,
,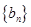 是等差数列,且
是等差数列,且 ,求非零常数
,求非零常数 ;
; ,求证:
,求证: .
.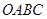 中,已知过点
中,已知过点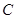 的直线与线段
的直线与线段 分别相交于点
分别相交于点 。若
。若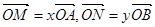 。
。 与
与 的关系为
的关系为 ;
; ,定义在
,定义在 上的偶函数
上的偶函数 ,当
,当 时
时 ,且函数
,且函数 对称,求证:
对称,求证: ,并求
,并求 时的解析式;
时的解析式; 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围。
的取值范围。 、
、 为坐标平面
为坐标平面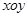 上的点,直线
上的点,直线 (
( 为坐标原点)与抛物线
为坐标原点)与抛物线 交于点
交于点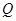 (异于
(异于 ,点
,点 上,试问当
上,试问当 为何值时,点
为何值时,点 在某一圆上,并求出该圆方程
在某一圆上,并求出该圆方程 ;
; 在椭圆
在椭圆 上,试问:点
上,试问:点 、
、 是圆
是圆 ,试问:是否存在一个定圆
,试问:是否存在一个定圆 ,使直线
,使直线 恒与圆
恒与圆 是
是 轴正方向的单位向量,设
轴正方向的单位向量,设 =
= ,
,  =
= ,且满足
,且满足 .
.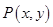 的轨迹方程;
的轨迹方程; 的直线
的直线 交上述轨迹于
交上述轨迹于 两点,且
两点,且 ,求直线
,求直线